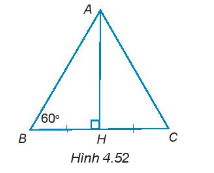
Cho tam giác ABH vuông tại đỉnh H có góc ABH = 60 độ. Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52)

Bài 4.47 trang 70 Tập 1: Cho tam giác ABH vuông tại đỉnh H có $\widehat{ABH}=60°$. Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH = $\frac{AB}{2}$.

Trả lời

+ Xét tam giác vuông ABH và tam giác vuông ACH có:

AH: cạnh chung

HB = HC (gt)

Do đó, ∆ABH = ∆ACH (hai cạnh góc vuông).

Suy ra AB = AC.   (1)

Do đó, tam giác ABC cân tại đỉnh A.

⇒ $\widehat{C}=\widehat{B}=\widehat{ABH}=60°$.

Ta có: $\widehat{BAC}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác).

Suy ra $\widehat{BAC}=180°-\widehat{B}-\widehat{C}$$=180°-60°-60°=60°$.

Khi đó $\widehat{B}=\widehat{BAC}$, do đó tam giác ABC cân tại đỉnh C nên  AC = BC. (2)

Từ (1) và (2) suy ra AB = AC = BC.

Do đó, ∆ABC đều.

+ Vì H thuộc BC và điểm H nằm giữa điểm B và điểm C, hơn nữa HB = HC, do đó H là trung điểm của BC.

Suy ra $BH=\frac{BC}{2}$.

Mà BC = AB (chứng minh trên).

Vậy BH = $\frac{AB}{2}$.