Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng: a) Hai đường trung tuyến BM, CN bằng nhau

Bài 4.45 trang 69 Tập 1: Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:

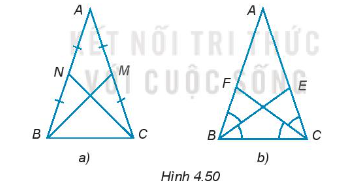
a) Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).

b) Hai đường phân giác BE, CF bằng nhau (H.4.50b).

Trả lời

a) Do BM và CN là đường trung tuyến của tam giác ABC nên M và N lần lượt là trung điểm của AC và AB.

Khi đó, $$\begin{gathered} AM=MC=\frac{AC}{2}; \\ AN=NB=\frac{AB}{2} \end{gathered}$$.

Mà AB = AC (do tam giác ABC cân tại đỉnh A).

Do đó, AM = MC = AN = NB.

Xét tam giác ABM và tam giác ACN có:

AB = AC

$\widehat{A}$: góc chung

AM = AN

Do đó, ∆ABM = ∆ACN (c – g – c).

Suy ra BM = CN (đpcm).

b) Do BE là đường phân giác của góc ABC nên $\widehat{ABE}=\frac{1}{2}\widehat{ABC}$.

Và CF là đường phân giác của góc ACB nên $\widehat{ACF}=\frac{1}{2}\widehat{ACB}$.

Lại có $\widehat{ABC}=\widehat{ACB}$ (do tam giác ABC cân tại đỉnh A).

Do đó, $\widehat{ABE}=\widehat{ACF}$.

Xét tam giác ABE và tam giác ACF có:

$\widehat{A}$: góc chung

AB = AC

$\widehat{ABE}=\widehat{ACF}$

Do đó, ∆ABE = ∆ACF (g – c – g)

Suy ra, BE = CF (đpcm).

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

Ôn tập chương 4

Bài 17: Thu thập và phân loại dữ liệu

Bài 18: Biểu đồ hình quạt tròn