Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB

Bài 9.68 trang 69 SBT Toán lớp 8 Tập 2: : Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB. Chứng minh rằng ∆CAM ᔕ ∆CBN và ∆CHM ᔕ ∆CAN.

Trả lời

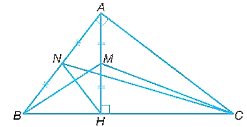
Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:  chung.

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{BC}{CA}=\frac{AB}{HA}=\frac{2BN}{2AM}=\frac{BN}{AM}$  (do M, N lần lượt là trung điểm của AH, AB).

Hay $\frac{AC}{CB}=\frac{AM}{BN}$ .

Xét tam giác CAM và tam giác CNB có:

 $\widehat{CAM}=\widehat{CBN}\left(=90°-\widehat{BAH}\right)$

$\frac{AC}{CB}=\frac{AM}{BN}$ (cmt)

Do đó, ∆CAM ᔕ ∆CBN (c.g.c).

Vì ∆ABC ᔕ ∆HAC nên ta có: $\frac{AC}{HC}=\frac{AB}{AH}=\frac{2AN}{2HM}=\frac{AN}{HM}$  hay $\frac{HC}{AC}=\frac{HM}{AN}$  .

Xét tam giác CHM vuông tại H và tam giác CAN vuông tại A có:

 $\frac{HC}{AC}=\frac{HM}{AN}$ (cmt)

Do đó, ∆CHM ᔕ ∆CAN (hai cạnh góc vuông).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: