Cho tam giác ABC vuông tại A có đường cao AH. a) Biết AB = 3 cm, AC = 4 cm, hãy tính độ dài các đoạn thẳng AH, BH, CH

Bài 9.66 trang 69 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH.

a) Biết AB = 3 cm, AC = 4 cm, hãy tính độ dài các đoạn thẳng AH, BH, CH.

b) Gọi M, N lần lượt là chân các đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng ∆HMN ᔕ ∆ABC.

Trả lời

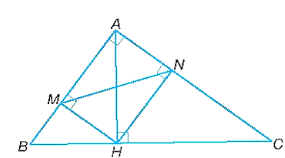
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 3² + 4² = 25 nên BC = 5 cm.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

 chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AC}{HC}=\frac{BC}{AC}$  nên $CH=\frac{C{A}^2}{CB}=\frac{4^2}{5}=\frac{16}{5}$  (cm).

Do đó, BH = BC – CH = 5 – $\frac{16}{5}$  = $\frac{9}{5}$  (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên $\frac{AB}{HA}=\frac{BC}{AC}$  

Do đó, $AH=\frac{AB\cdot AC}{BC}=\frac{3\cdot 4}{5}=\frac{12}{5}$   (cm).

b)

Vì HM vuông góc AB, suy ra $\widehat{HMA}=90°$ .

HN vuông góc với AC, suy ra $\widehat{HNA}=90°$ .

Tứ giác ANHM có: $\widehat{HMA}=\widehat{NAM}=\widehat{HNA}=90{°}_{}$ nên tứ giác ANHM là hình chữ nhật.

Do đó, $\widehat{NHM}=90°$ .

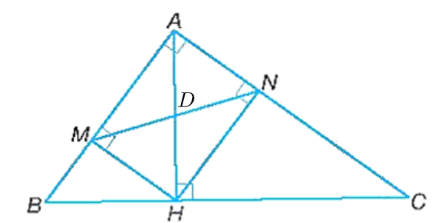
Gọi D là giao điểm của hai đường chéo trong hình chữ nhật NHMA nên DH = DM. Do đó, tam giác DHM cân tại D.

Suy ra: $\widehat{DHM}=\widehat{DMH}$

Lại có: $\widehat{DHM}=\widehat{B}\left(=90°-\widehat{MHB}\right)$  nên $\widehat{DMH}=\widehat{B}$ .

Xét tam giác HMN vuông tại H và tam giác ABC vuông tại A có:

$\widehat{NMH}=\widehat{B}$ (do $\widehat{DMH}=\widehat{B}$  )

Do đó, ∆HMN ᔕ ∆ABC (góc nhọn).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: