Cho tam giác ABC với AB > AC. Lấy điểm D trên cạnh AB sao cho AC = AD. Qua D kẻ đường thẳng song song với BC và cắt AC tại E

Bài 9.64 trang 68 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB > AC. Lấy điểm D trên cạnh AB sao cho AC = AD. Qua D kẻ đường thẳng song song với BC và cắt AC tại E. Qua E kẻ đường thẳng song song với CD và cắt AB tại F. Chứng minh rằng:

a) AD² = AF . AB.

b) ∆ACF ᔕ ∆ABC.

Chú ý: Đề trong sách cho D thuộc cạnh BC là sai, cần sửa như trên.

Trả lời

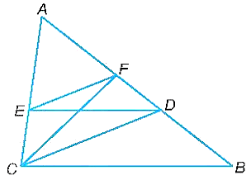
a)

Tam giác ABC có: DE song song với BC nên ∆ADE ᔕ ∆ABC.

Do đó, $\frac{AD}{AB}=\frac{AE}{AC}$   hay AD = $\frac{AB\cdot AE}{AC}$   (1).

Tam giác ADC có: FE song song với DC nên ∆AFE ᔕ ∆ADC.

Do đó, $\frac{AF}{AD}=\frac{AE}{AC}$  , hay AD = $\frac{AF\cdot AC}{AE}$   (2).

Từ (1) và (2) ta có: $A{D}^2=\frac{AB\cdot AE}{AC}\cdot \frac{AF\cdot AC}{AE}=AB\cdot AF$  .

b) Theo câu a có $\frac{AF}{AD}=\frac{AE}{AC}$   và AD = AC (gt), suy ra AE = AF.

Lại có $\frac{AD}{AB}=\frac{AE}{AC}$   nên $\frac{AC}{AB}=\frac{AE}{AD}=\frac{AE}{AC}=\frac{AF}{AC}$  (do AC = AD và AE = AF).

Xét tam giác ACF và tam giác ABC có:

 $\widehat{A}$ chung

 $\frac{AC}{AB}=\frac{AF}{AC}$ (chứng minh trên)

Do đó, ∆ACF ᔕ ∆ABC (c.g.c).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: