Bài 4 trang 87 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Gọi D là trung điểm của BC. Vẽ DE // AB, vẽ DF // AC (E ∈ AC, F ∈ AB). Chứng minh rằng:
a) Tứ giác AEDF là hình chữ nhật.
b) Tứ giác BFED là hình bình hành.
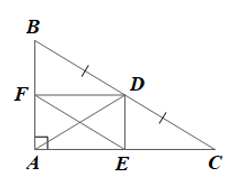
a) Tam giác ABC vuông tại A nên hay AB ⊥ AC.
Do DE // AB và AB ⊥ AC nên DE ⊥ AC hay .
Do DF // AC và AB ⊥ AC nên DF ⊥ AB hay
Tứ giác AEDF có , và nên là hình chữ nhật.
b) Do AEDF là hình chữ nhật nên AF = ED và AD = EF (tính chất hình chữ nhật).
Xét DABC có AD là đường trung tuyến ứng với cạnh huyền BC nên bằng nửa cạnh huyền BC, do đó .
Từ đó suy ra
Xét DBDF và DEFD có:
;
BD = EF (chứng minh trên);
DF là cạnh chung.
Do đó DBDF = DEFD (cạnh huyền – cạnh góc vuông).
Suy ra FB = DE (hai cạnh tương ứng).
Xét tứ giác BFED có FB = DE và FB // DE (do AB // DE) nên là hình bình hành.
Xem thêm lời giải bài tập SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Hình thang – Hình thang cân
Bài 4: Hình bình hành – Hình thoi