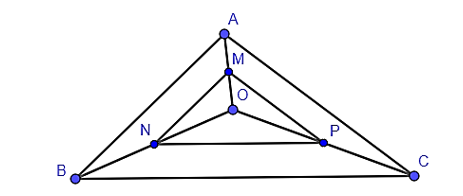
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi M, N, P lần lượt là trung điểm
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi M, N, P lần lượt là trung điểm của các đoạn OA, OB, OC. Khi đó tam giác MNP đồng dạng với tam giác nào?
A. Tam giác ABC;
B. Tam giác OMN;
C. Tam giác OBC;