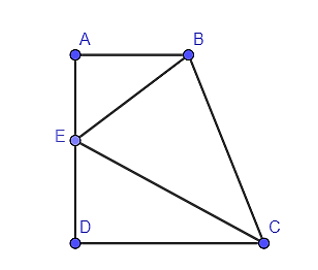
Cho hình thang vuông ABCD tại A và D, AB = 6 cm, CD = 12 cm, AD = 17 cm. Trên cạnh AD lấy

B. 45°;

C. 90.°;

Trả lời

Hướng dẫn giải:

Đáp án đúng là: C

Ta có AD = AE + ED nên ED = AD – AE = 17 – 8 = 9 (cm).

Có $\frac{\text{AB}}{\text{DE}}=\frac{6}{9}=\frac{2}{3},\frac{\text{BE}}{\text{EC}}=\frac{10}{15}=\frac{2}{3}$.

Suy ra $\frac{\text{AB}}{\text{DE}}=\frac{\text{BE}}{\text{EC}}$.

Xét hai tam giác ABE và DEC có:

$\widehat{\text{BAE}}=\widehat{\text{EDC}}=90°$

$\frac{\text{AB}}{\text{DE}}=\frac{\text{BE}}{\text{EC}}$

Suy ra ΔABE ᔕ ΔDEC (ch – cgv).

Suy ra $\widehat{\text{AEB}}=\widehat{\text{ECD}}$.

Mà $\widehat{\text{DEC}}+\widehat{\text{ECD}}=90°$ (do tam giác DEC vuông tại D) nên $\widehat{\text{DEC}}+\widehat{\text{AEB}}=90°$.

Suy ra $\widehat{\text{BEC}}=180°-\left(\widehat{\text{DEC}}+\widehat{\text{AEB}}\right)=180°-90°=90°$.