Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự nào sau đây biến tam giác ABC thành tam giác MNP? A. Phép vị tự tâm A, tỉ số k = 1/2
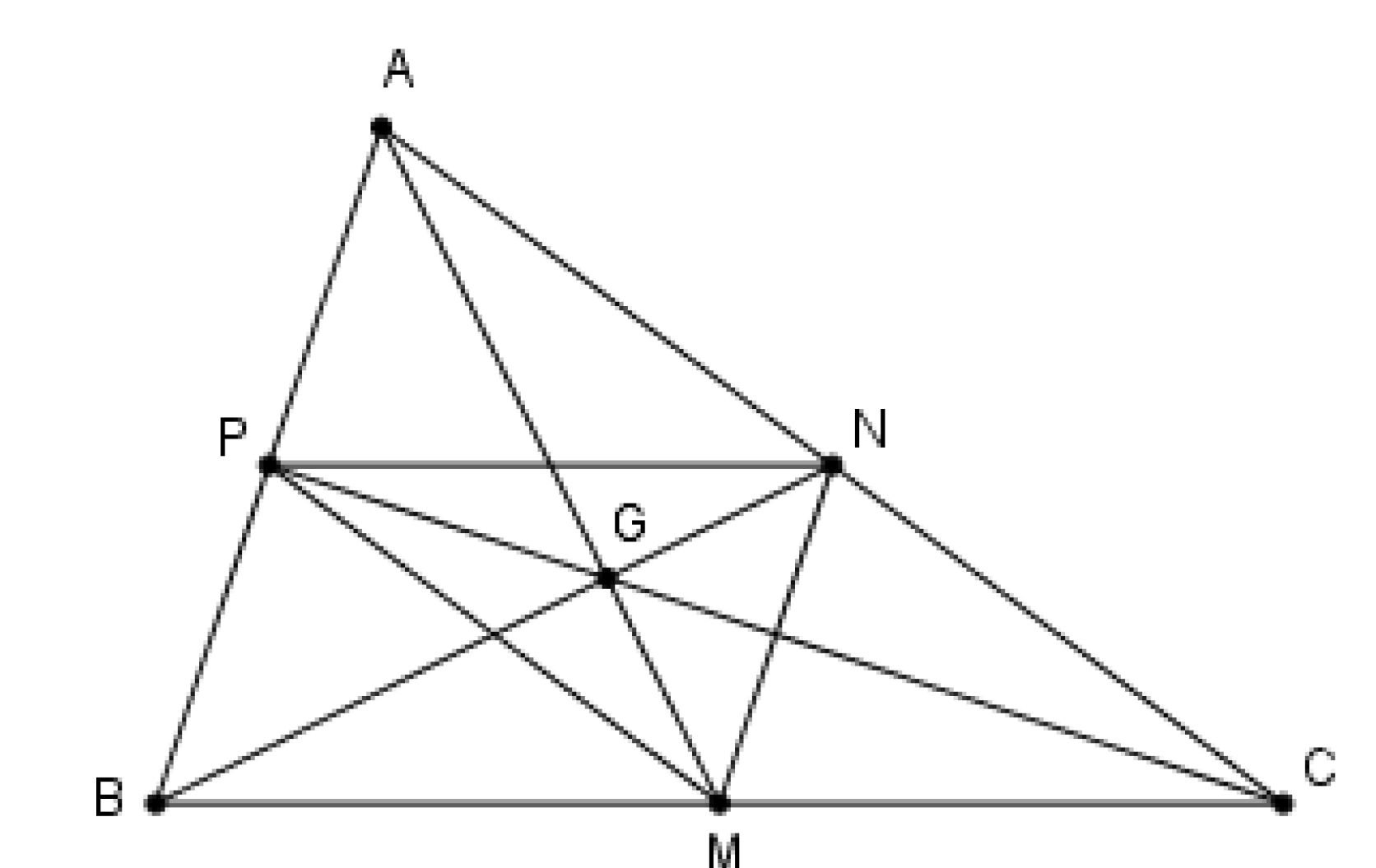
Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự nào sau đây biến tam giác ABC thành tam giác MNP?
A. Phép vị tự tâm A, tỉ số k=12
B. Phép vị tự tâm G, tỉ số k=−12
C. Không có phép vị tự nào
D. Phép vị tự tâm G, tỉ số k=12