Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC

Bài 10 trang 96 Toán 8 Tập 2: Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC. Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN, AI và BC. Chứng minh:

a) $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}};$                 

b) $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}.$

Trả lời

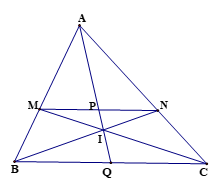
a) Vì MN // BC, P ∈ MN nên ta có: MP // BQ, PN // QC.

Xét ∆ABQ với MP // BQ, ta có: $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{AP}}{\mathrm{AQ}}$  (hệ quả của định lí Thalès)

Xét ∆AQC với PN // QC, ta có: $\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}}$  (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}}.$

b) Vì MN // BC nên ta có: MP // QC, PN // BQ.

Xét ∆CQI với MP // QC, ta có: $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{IP}}{\mathrm{IQ}}$  (hệ quả của định lí Thalès)

Xét ∆BQI với PN // BQ, ta có: $\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}$  (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}.$

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn

Bài tập cuối chương 8

Chủ đề 3: Thực hành đo chiều cao