Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN

Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:

a) MP // AD, $\mathrm{MP}=\frac{1}{4}\mathrm{AD};$

b) $\mathrm{AQ}=\frac{2}{5}\mathrm{AN};$

c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và  $\mathrm{PR}=\frac{3}{4}\mathrm{AD}.$  

Trả lời

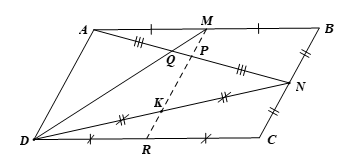
a)  Do N là trung điểm của BC nên $\mathrm{BN}=\frac{1}{2}\mathrm{BC}$

Và ABCD là hình bình hành nên BC = AD, BC // AD

Suy ra  $\mathrm{BN}=\frac{1}{2}\mathrm{AD},\mathrm{BN}\text{ // }\mathrm{AD}$ (1)

Xét ∆ABN có M, P lần lượt là trung điểm của AB, AN nên MP là đường trung bình của ∆ABN

Suy ra $\mathrm{MP}=\frac{1}{2}\mathrm{BN}$  và MP // BN         (2)

Từ (1) và (2) ta có $\mathrm{MP}=\frac{1}{2}\mathrm{BN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{AD}=\frac{1}{4}\mathrm{AD}$  và MP // AD.

Vậy MP // AD và $\mathrm{MP}=\frac{1}{4}\mathrm{AD}.$  (3)

b) Xét ∆ADQ với MP // AD, ta có $\frac{\mathrm{AD}}{\mathrm{MP}}=\frac{\mathrm{QA}}{\mathrm{QP}}$  (hệ quả của định lí Thalès)

Hay $\frac{\mathrm{AD}}{\frac{1}{4}\mathrm{AD}}=\frac{\mathrm{AQ}}{\mathrm{PQ}}$  nên $\frac{\mathrm{AQ}}{\mathrm{PQ}}=\frac{4}{1}$

Suy ra $\frac{\mathrm{AQ}}{\mathrm{PQ}+\mathrm{AQ}}=\frac{4}{1+4}$  hay $\frac{\mathrm{AQ}}{\mathrm{AP}}=\frac{4}{5}$

Mà P là trung điểm của AN nên $\mathrm{AP}=\frac{1}{2}\mathrm{AN}$

Do đó $\frac{\mathrm{AQ}}{\frac{1}{2}\mathrm{AN}}=\frac{4}{5},$  suy ra $\mathrm{AQ}=\frac{4}{5}\cdot \frac{1}{2}\mathrm{AN}=\frac{2}{5}\mathrm{AN}.$

Vậy $\mathrm{AQ}=\frac{2}{5}\mathrm{AN}.$

c) Gọi K là trung điểm của DN.

Xét ∆AND có P, K lần lượt là trung điểm của AN, DN nên PK là đường trung bình của ∆AND. Do đó PK // AD và $\mathrm{PK}=\frac{1}{2}\mathrm{AD}$    (4)

Tương tự, xét ∆CDN có KR là đường trung bình của ∆CDN nên KR // CN và $\mathrm{KR}=\frac{1}{2}\mathrm{CN}$    

Mà N là trung điểm của BC nên $\mathrm{CN}=\frac{1}{2}\mathrm{BC}=\frac{1}{2}\mathrm{AD}$  và BC // AD

Do đó KR // AD và $\mathrm{KR}=\frac{1}{2}\mathrm{CN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{AD}=\frac{1}{4}\mathrm{AD}$  (5)

Từ (3), (4) và (5), theo tiên đề Euclid ta có: M, P, K, R thẳng hàng.

Và $\mathrm{PR}=\mathrm{PK}+\mathrm{KR}=\frac{1}{2}\mathrm{AD}+\frac{1}{4}\mathrm{AD}=\frac{3}{4}\mathrm{AD}.$

Vậy ba điểm M, P, R thẳng hàng và $\mathrm{PR}=\frac{3}{4}\mathrm{AD}.$

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn

Bài tập cuối chương 8

Chủ đề 3: Thực hành đo chiều cao