Cho tam giác ABC có , M là trung điểm của BC. Chứng minh BC = 2AMQua C kẻ đường thẳng d song song với
Bài 42* trang 81 SBT Toán 7 Tập 2: Cho tam giác ABC có , M là trung điểm của BC. Chứng minh BC = 2AM.
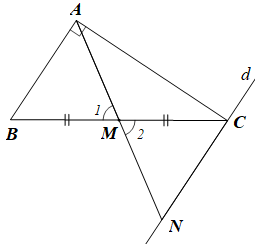
Qua C kẻ đường thẳng d song song với AB, d cắt AM tại N.
Suy ra (hai góc so le trong).
Ta có BA ⊥ AC, d // AB.
Suy ra d ⊥ AC hay .
Xét MBA và MCN có:
BM = CM (vì M là trung điểm của BC),
(hai góc đối đỉnh),
(chứng minh trên)
Do đó ∆MBA = ∆MCN (g.c.g).
Suy ra AB = CN và AM = NM (các cặp cạnh tương ứng).
Xét BAC và NCA có:
AC là cạnh chung,
(cùng bằng 90
),
AB = NC (chứng minh trên)
Do đó ∆BAC = ∆NCA (c.g.c)
Suy ra BC = NA (hai cạnh tương ứng).
Mà AM = MN, AN = AM + MN = 2AM.
Nên BC = AN = 2AM.
Vậy 2AM = BC.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6. Trường hợp bằng nhau thứ ba của tam giác: