Cho tam giác ABC có ba góc đều nhọn và góc A = 60 độ  Tia phân giác của góc ABC cắt AC tại D, tia phân giác của góc ACB cắt AB tại E

Bài 41 trang 81 SBT Toán 7 Tập 2: Cho tam giác ABC có ba góc đều nhọn và $\widehat{A}=60°.$ Tia phân giác của góc ABC cắt AC tại D, tia phân giác của góc ACB cắt AB tại E. BD cắt CE tại I. Tia phân giác của góc BIC cắt BC tại F. Chứng minh:

a) $\widehat{BIC}=120°$;

b) ∆BEI = ∆BFI;

c) BC = BE + CD.

Trả lời

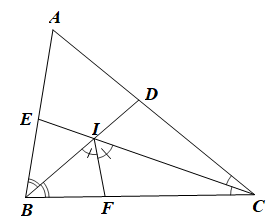
a) Vì BD là phân giác của góc ABC nên $\widehat{ABD}=\widehat{CBD}=\frac{\widehat{ABC}}{2}$.

Vì CE là phân giác của góc ACB nên $\widehat{ACE}=\widehat{ECB}=\frac{\widehat{ACB}}{2}$.

Xét $∆$ABC có: $\widehat{A}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{ABC}+\widehat{ACB}=180°-\widehat{A}=180°-60°=120°$

Xét $∆$IBC có: $\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180°$ (tổng ba góc của một tam giác)

Hay $\widehat{BIC}+\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}=180°$

Suy ra $\widehat{BIC}=180°-\frac{\widehat{ABC}+\widehat{ACB}}{2}=180°-\frac{120°}{2}=120°$

Vậy $\widehat{BIC}=120°.$

b) Vì IF là phân giác của góc BIC nên $\widehat{BIF}=\widehat{CIF}=\frac{\widehat{BIC}}{2}=\frac{120°}{2}=60°$

Ta có $\widehat{BIC}+\widehat{BIE}=180°$ (hai góc kề bù)

Suy ra $\widehat{BIC}=180°-\frac{\widehat{ABC}+\widehat{ACB}}{2}=180°-\frac{120°}{2}=120°$

Xét $∆$BEI và $∆$BFI có:

$\widehat{EBI}=\widehat{FBI}$ (chứng minh câu a),

BI là cạnh chung,

$\widehat{EIB}=\widehat{FIB}$ (cùng bằng 60°),

Do đó ∆BEI = ∆BFI (g.c.g).

Vậy ∆BEI = ∆BFI.

c) Do ∆BEI = ∆BFI (câu b) nên BE = BF (hai cạnh tương ứng).

Ta có $\widehat{BIC}+\widehat{CID}=180°$ (hai góc kề bù)

Suy ra $\widehat{CID}=180°-\widehat{BIC}=180°-120°=60°$.

Xét $∆$CFI và $∆$CDI có:

$\widehat{FCI}=\widehat{DCI}$ (chứng minh câu a),

CI là cạnh chung,

$\widehat{CIF}=\widehat{CID}$ (cùng bằng 60°),

Suy ra ∆CFI = ∆CDI (g.c.g).

Do đó CF = CD (hai cạnh tương ứng).

Ta có: BC = BF + FC = BE + CD.

Vậy BC = BE + CD.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6. Trường hợp bằng nhau thứ ba của tam giác:

Bài 7. Tam giác cân

Bài 8. Đường vuông góc và đường xiên

Bài 9. Đường trung trực của một đoạn thẳng