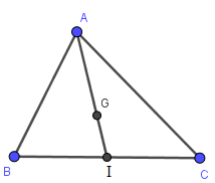
Cho tam giác ABC có B, C cố định, đỉnh A chạy trên một đường tròn ( O; R) cố định không có điểm chung với đường thẳng BC và G là trọng tâm tam giác ABC. Khi đó quỹ tích trọng tâm G là ảnh của
Cho tam giác ABC có B, C cố định, đỉnh A chạy trên một đường tròn \[\left( {O;\,\,R} \right)\] cố định không có điểm chung với đường thẳng BC và G là trọng tâm tam giác ABC. Khi đó quỹ tích trọng tâm G là ảnh của đường tròn \[\left( {O;\,\,R} \right)\] qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ \[\overrightarrow {BC} \]
B. Phép vị tự tâm I tỷ số \[k = 3\], trong đó I là trung điểm của BC
C. Phép vị tự tâm I tỷ số \[k = \frac{1}{3}\], trong đó I là trung điểm của BC
D. Phép tịnh tiến theo véc tơ \[\overrightarrow v = \frac{1}{3}\overrightarrow {IA} \]