Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6. Chứng minh rằng:

\[\widehat {ABN} = \widehat {ACM}\].

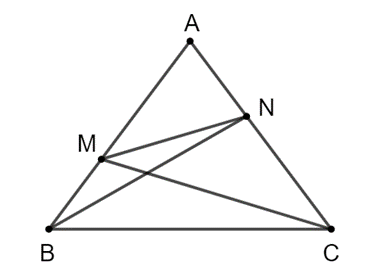
Ta có \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\], suy ra \[\frac{{AN}}{{AM}} = \frac{{AB}}{{AC}}\].

Xét ∆ANB và ∆AMC có

\[\frac{{AN}}{{AM}} = \frac{{AB}}{{AC}}\] và \[\widehat A\] chung.

Do đó ∆ANB ᔕ ∆AMC (c.g.c).

Suy ra \[\widehat {ABN} = \widehat {ACM}\] (hai góc tương ứng).