Cho tam giác ABC cân tại A có H là hình chiếu của A trên đường thẳng BC, lấy điểm M nằm giữa A và H. Chứng minh

Bài 53 trang 85 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có H là hình chiếu của A trên đường thẳng BC, lấy điểm M nằm giữa A và H. Chứng minh:

a) BH = CH;

b) MB = MC;

c) MA < AC.

Trả lời

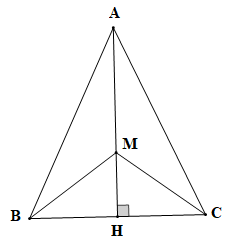
a) Vì tam giác ABC cân tại A nên AB = AC.

Xét $∆$AHB và $∆$AHC có:

$\widehat{AHB}=\widehat{AHC}\left(=90°\right)$,

BA = AC (chứng minh trên),

AH là cạnh chung

Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông).

Suy ra BH = CH (hai cạnh tương ứng).

Vậy BH = CH.

b) Vì ∆ABH = ∆ACH (chứng minh câu a)

Suy ra $\widehat{HAB}=\widehat{HAC}$ (hai góc tương ứng).

Xét $∆$AMB và $∆$AMC có:

BA = AC (chứng minh câu a),

$\widehat{MAB}=\widehat{MAC}$ (do $\widehat{HAB}=\widehat{HAC}$),

AM là cạnh chung

Do đó ∆ABM = ∆ACM (c.g.c).

Suy ra BM = CM (hai cạnh tương ứng).

Vậy BM = CM.

c) Vì $\widehat{AMC}$ là góc ngoài của tam giác CMH tại đỉnh M

Nên $\widehat{AMC}=\widehat{MHC}+\widehat{MCH}$

Mà $\widehat{MHC}=90°$ nên $\widehat{AMC}$ là góc tù

Xét tam giác AMC có $\widehat{AMC}$ là góc tù

Nên MC < AC (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất).

Vậy MC < AC.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 6. Trường hợp bằng nhau thứ ba của tam giác:

Bài 7. Tam giác cân

Bài 8. Đường vuông góc và đường xiên

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác

Bài 11. Tính chất ba đường phân giác của tam giác