Cho tam giác ABC. a) Tìm điểm M sao cho MA + MB + 2.MC = 0; b) Xác định điểm N
Bài 4.19 trang 54 SBT Toán 10 Tập 1:
Cho tam giác ABC.
a) Tìm điểm M sao cho →MA+→MB+2→MC=→0.
b) Xác định điểm N thoả mãn 4→NA−2→NB+→NC=→0.
a)
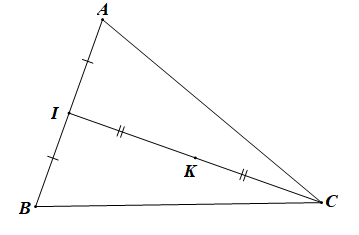
Gọi I là trung điểm của AB.
Khi đó: →MA+→MB=2→MI
⇒→MA+→MB+2→MC=2→MI+2→MC=2(→MI+→MC)
Gọi K là trung điểm của IC, khi đó: →MI+→MC=2→MK
⇒→MA+→MB+2→MC=2.2→MK=4→MK.
Mà →MA+→MB+2→MC=→0.
Do đó 4→MK=→0⇔→MK=→0
Suy ra M ≡ K.
Vậy M là trung điểm của IC (với I là trung điểm của AB).
b)
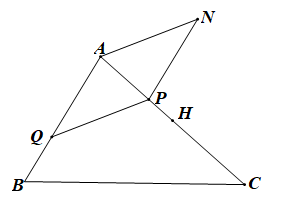
Ta có:
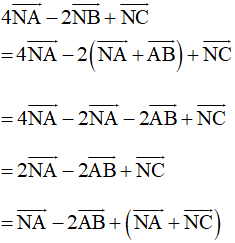
Gọi H là trung điểm của AC, khi đó
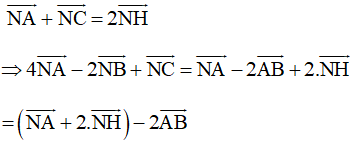
Giả sử P là điểm thỏa mãn →PA+2.→PH=→0
Khi đó
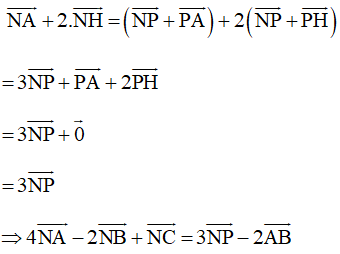
Mà 4→NA−2→NB+→NC=→0.
Nên
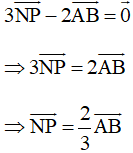
Gọi Q là điểm nằm trên cạnh AB sao cho →AQ=23→AB
⇒→NP=→AQ
Do đó tứ giác AQPN là hình bình hành
Vậy điểm N cần tìm là đỉnh của hình bình hành AQPN (với Q thỏa mãn →AQ=23→AB và P thỏa mãn →PA+2.→PH=→0, H là trung điểm của AC).
Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vectơ với một số
Bài 10: Vectơ trong mặt phẳng tọa độ