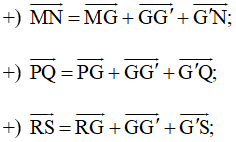Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA

Bài 4.17 trang 54 SBT Toán 10 Tập 1:

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S theo thứ tự là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Trả lời

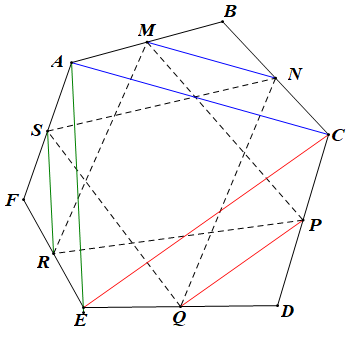
+) Vì M, N lần lượt là trung điểm của AB, BC

Nên MN là đường trung bình của tam giác ABC.

$\Rightarrow$ MN // AC và $MN=\frac{1}{2}AC$ (tính chất đường trung bình)

Do đó $\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AC}$                                                (1)

Chứng minh tương tự ta cũng có: $\overrightarrow{PQ}=\frac{1}{2}\overrightarrow{CE}$         (2)

Và $\overrightarrow{RS}=\frac{1}{2}\overrightarrow{EA}$                                                       (3)

Từ (1), (2) và (3) ta có:

$$\begin{gathered} \overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RS} \\ =\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CE}+\frac{1}{2}\overrightarrow{EA} \end{gathered}$$

$=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{EA}\right)$ 

$=\frac{1}{2}\left(\overrightarrow{AE}+\overrightarrow{EA}\right)$ (quy tắc ba điểm)

$=\frac{1}{2}\overrightarrow{\text{AA}}$                 (quy tắc ba điểm)

$=\frac{1}{2}.\overrightarrow{0}=\overrightarrow{0}$

Do đó $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RS}=\overrightarrow{0}$

+) Giả sử G và G' lần lượt là trọng tâm của tam giác MPR và tam giác NQS.

Khi đó ta có: $\overrightarrow{MG}+\overrightarrow{PG}+\overrightarrow{RG}=\overrightarrow{0}$ và $\overrightarrow{N{G}^{\text{'}}}+\overrightarrow{Q{G}^{\text{'}}}+\overrightarrow{S{G}^{\text{'}}}=\overrightarrow{0}$ hay $\overrightarrow{G^{\text{'}}N}+\overrightarrow{G^{\text{'}}Q}+\overrightarrow{G^{\text{'}}S}=\overrightarrow{0}$

Mặt khác: theo quy tắc ba điểm ta có:

$$\begin{gathered} \Rightarrow \overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RS} \\ =\overrightarrow{MG}+\overrightarrow{PG}+\overrightarrow{RG}+3.\overrightarrow{G{G}^{\text{'}}}+\overrightarrow{G^{\text{'}}N}+\overrightarrow{G^{\text{'}}Q}+\overrightarrow{G^{\text{'}}S} \end{gathered}$$

$=\left(\overrightarrow{MG}+\overrightarrow{PG}+\overrightarrow{RG}\right)+3.\overrightarrow{G{G}^{\text{'}}}+\left(\overrightarrow{G^{\text{'}}N}+\overrightarrow{G^{\text{'}}Q}+\overrightarrow{G^{\text{'}}S}\right)$

$=\overrightarrow{0}+3.\overrightarrow{G{G}^{\text{'}}}+\overrightarrow{0}$

$=3.\overrightarrow{G{G}^{\text{'}}}$

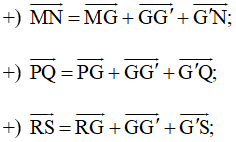
+) Lại có $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RS}=\overrightarrow{0}$ (chứng minh trên)

Nên $3\overrightarrow{G{G}^{\text{'}}}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{G{G}^{\text{'}}}=\overrightarrow{0}$

Suy ra G và G' trùng nhau.

Vậy hai tam giác MPR và NQS có cùng trọng tâm.

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4