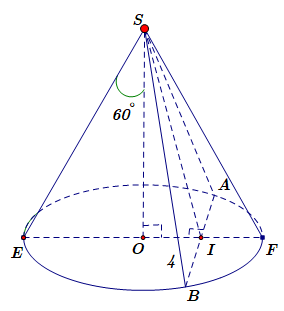
Cho khối nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 độ. Một mặt phẳng (P) đi qua S,
Cho khối nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng . Một mặt phẳng (P) đi qua S, cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 4. Tính thể tích V của khối nón (N).
A.
B.
C.
D.