Cho khối chóp S.ABCD có đáy là hình bình hành AB = 3, AD = 4, góc BAD = 120 độ. Cạnh bên SA = 2 căn 3 và vuông góc với mặt phẳng (ABCD).

A. $\alpha \in \left(0°;30°\right)$

B. $\alpha \in \left(30°;45°\right)$

C. $\alpha \in \left(45°;60°\right)$

D. $\alpha \in \left(60°;90°\right)$

Trả lời

Đáp án đúng là: D

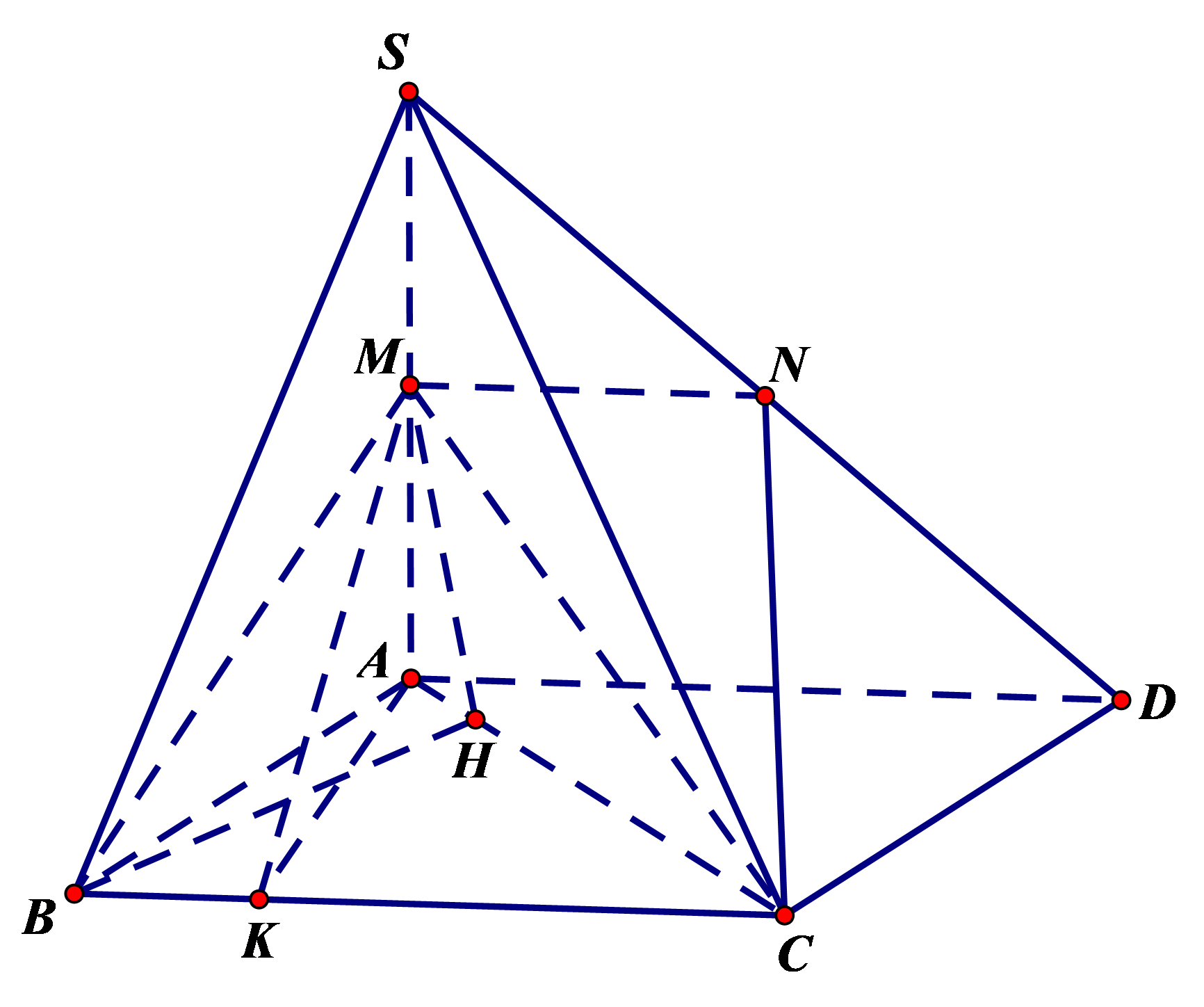
Với mọi điểm $P\in BC$ ta có $\left(MNP\right)\equiv \left(BCNM\right)\equiv \left(MBC\right)$ , do đó góc giữa hai mặt phẳng (SAC) và (MNP) bằng góc giữa hai mặt phẳng (SAC) và (MBC).

Gọi H là hình chiếu của B lên AC thì $BH\perp \left(SAC\right)$  nên $\Delta MHC$  là hình chiếu của $\Delta MBC$  lên (SAC).

Do đó $S_{\Delta MHC}=S_{\Delta MBC}.\cos \alpha$ ; $\left(\left(MBC\right),\left(SAC\right)\right)=\alpha$ .

Gọi K là hình chiếu của A lên BC thì $MK\perp BC$ .

Ta có $AK=AB.\sin \widehat{ABK}=3.\sin 60°=\frac{3\sqrt{3}}{2}$

$\Rightarrow MK=\sqrt{M{A}^2+A{K}^2}=\frac{\sqrt{39}}{2}\Rightarrow S_{\Delta MBC}=\frac{1}{2}BC.MK=\sqrt{39}$

.

Ta có $KB=AB.\cos \widehat{ABK}=\frac{3}{2}\Rightarrow KC=\frac{5}{2}$

$\Rightarrow AC=\sqrt{A{K}^2+K{C}^2}=\sqrt{13}\Rightarrow BH=\frac{BC.AK}{AC}=\frac{6\sqrt{39}}{13}$

$\Rightarrow CH=\sqrt{B{C}^2-B{H}^2}=\frac{10\sqrt{13}}{13}$$\Rightarrow S_{\Delta MHC}=\frac{1}{2}CH.MA=\frac{5\sqrt{39}}{13}$

Suy ra $\cos \alpha =\frac{S_{\Delta MHC}}{S_{\Delta MBC}}=\frac{5\sqrt{39}}{13\sqrt{39}}=\frac{5}{13}\Rightarrow \alpha \in \left(60°;90°\right)$ .