Cho hình vuông ABCD tâm I. Gọi M, N lần lượt là trung điểm của AD, DC. Phép tịnh tiến theo vectơ nào sau đây biến Delta AMI thành Delta MDN? A. vecto AC B. vecto AM C. vecto NI D.
38
23/04/2024
Cho hình vuông ABCD tâm I. Gọi M, N lần lượt là trung điểm của AD, DC. Phép tịnh tiến theo vectơ nào sau đây biến \(\Delta AMI\) thành \(\Delta MDN\)?
A. \(\overrightarrow {AC} .\)
B. \(\overrightarrow {AM} .\)
C. \(\overrightarrow {NI} .\)
D. \(\overrightarrow {MN} .\)
Trả lời
Đáp án B
Phương pháp:
Phép tịnh tiến biến tam giác này thành tam giác kia là phép tịnh tiến biến mỗi đỉnh của tam giác này thành mỗi đỉnh tương ứng của tam giác kia.
Cách giải:
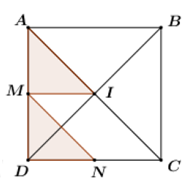
Ta có: IN là đường trung bình của tam giác \(ACD \Rightarrow IN = \frac{1}{2}AD = AM.\)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {IN} = {T_{\overrightarrow {AM} }}\left( I \right) = N.\)
Dễ thấy \(\overrightarrow {AM} = \overrightarrow {MD} \Rightarrow {T_{\overrightarrow {AM} }}\left( M \right) = D\) và hiển nhiên \({T_{\overrightarrow {AM} }}\left( A \right) = M.\)
Vậy \({T_{\overrightarrow {AM} }}\left( {\Delta AMI} \right) = \Delta MDN.\)
