Cho hình vuông ABCD, M là trung điểm của BC, N là điểm nằm giữa hai điểm A và C

Bài 64* trang 106 SBT Toán 10 Tập 1: Cho hình vuông ABCD, M là trung điểm của BC, N là điểm nằm giữa hai điểm A và C. Đặt x = $\frac{AN}{AC}$. Tìm x thỏa mãn AM ⊥ BN.

Trả lời

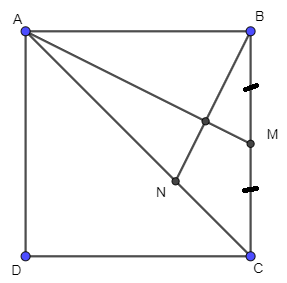
Gọi a là độ dài cạnh của hình vuông ABCD

Vì M là trung điểm của BC nên ta có:

$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$

⇔ $\overrightarrow{AM}=\overrightarrow{BM}-\overrightarrow{BA}=\frac{1}{2}\overrightarrow{BC}-\overrightarrow{BA}$

Ta lại có:

$$\begin{gathered} \overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{AN}=-\overrightarrow{AB}+x\overrightarrow{AC} \\ =-\overrightarrow{AB}+x\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=(1-x)\overrightarrow{BA}+x\overrightarrow{BC} \end{gathered}$$

⇒ $\overrightarrow{AM}.\overrightarrow{BN}=\left(\frac{1}{2}\overrightarrow{BC}-\overrightarrow{BA}\right)$$\left[(1-x)\overrightarrow{BA}+x\overrightarrow{BC}\right]$

⇔ $\overrightarrow{AM}.\overrightarrow{BN}=\frac{1}{2}(1-x)\overrightarrow{BC}.\overrightarrow{BA}+$$\frac{1}{2}x{\overrightarrow{BC}}^2-\left(1-x\right){\overrightarrow{BA}}^2-x\overrightarrow{BA}.\overrightarrow{BC}$

⇔ $\overrightarrow{AM}.\overrightarrow{BN}=\frac{1}{2}x.a^2-\left(1-x\right)a^2$

⇔ $\overrightarrow{AM}.\overrightarrow{BN}=\left(\frac{3}{2}x-1\right)a^2$

Để AM vuông góc với BN thì $\overrightarrow{AM}.\overrightarrow{BN}=0$

⇔ $\left(\frac{3}{2}x-1\right)a^2=0$

⇔ $\frac{3}{2}x-1=0$

⇔ $x=\frac{2}{3}$

Vậy với $x=\frac{2}{3}$ thì AM ⊥ BN.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài ôn tập chương 4

Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Bài 2: Hoán vị. Chỉnh hợp