Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC
814
08/05/2023
Bài 14 trang 96 Toán 10 Tập 2: Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
a) Biểu thị các vectơ →DM, →AN theo các vectơ →AB, →AD.
b) Tính →DM ⋅ →AN và tìm góc giữa hai đường thẳng DM và AN.
Trả lời
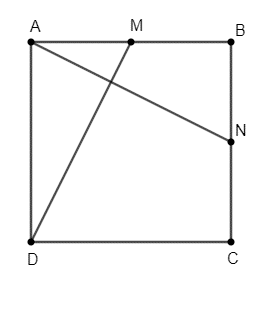
a) Vì M là trung điểm của AB nên →AM=12→AB.
Do đó, ta có: →DM=→AM−→AD=12→AB−→AD.
Vì N là trung điểm của BC nên →BN=12→BC.
Do ABCD là hình vuông nên →BC=→AD. Khi đó, →BN=12→AD.
Theo quy tắc ba điểm ta có: →AN=→AB+→BN=→AB+12→AD.
b) Do ABCD là hình vuông nên ta có: AB = AD = a,→AB ⋅ →AD=0 (AB ⊥ AD).
Từ đó suy ra →DM ⋅ →AN=(12→AB−→AD)⋅ (→AB+12→AD)
=12(→AB)2+14→AB⋅ →AD−→AD⋅ →AB−12(→AD)2.
=12AB2+14⋅ 0−0−12AD2
=12(AB2−AD2)=0
Do đó: →DM ⋅ →AN=0⇔→DM⊥→AN⇔DM⊥AN.
Vậy góc giữa hai đường thẳng DM và AN bằng 90°.

