Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48). ∆ABD có cân tại A không

HĐ1 trang 68 Toán 8 Tập 1: Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48).

a) ∆ABD có cân tại A không?

b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao?

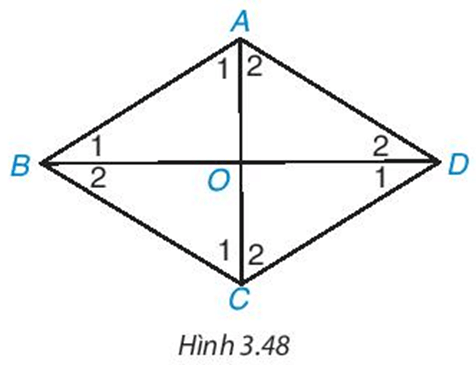
Trả lời

a) Vì tứ giác ABCD là hình thoi nên AB = AD.

Suy ra ∆ABD có cân tại A.

b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA.

Xét ∆ABC và ∆ADC có:

AB = AD (chứng minh trên);

BC = CD (chứng minh trên);

Cạnh AC chung.

Do đó ∆ABC = ∆ADC (c.c.c)

Suy ra ${\hat{A}}_1={\hat{A}}_2$ (hai góc tương ứng)

Hay AC là đường phân giác của góc A.

Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao.

Khi đó AO ⊥ BD hay AC ⊥ BD.

Vậy AC vuông góc với BD và AC là đường phân giác của góc A.

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác: