Cho hình thang ABCD (AB // CD) có góc DAB = góc DBC. a) Chứng minh rằng ΔABD ∽ ΔBDC

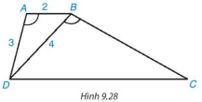
Bài 9.13 trang 92 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có  $\widehat{DAB}=\widehat{DBC}$.

a) Chứng minh rằng ΔABD ∽ ΔBDC. 

b) Giả sử AB = 2 cm, AD = 3 cm, BD = 4 cm. Tính độ dài các cạnh BC và DC.

Trả lời

a) Vì AB // CD (giả thiết) nên $\widehat{ABD}=\widehat{BDC}$(2 góc ở vị trí so le trong).

+ Xét ΔABD và ΔBDC có: $\widehat{ABD}=\widehat{BDC},\widehat{DAB}=\widehat{DBC}$.

Suy ra ΔABD ∽ ΔBDC (g.g).

b) Ta có: $\frac{AB}{BD}=\frac{2}{4}=\frac{1}{2}$.

Vậy ΔABD ∽ ΔBDC với tỉ số đồng dạng $\frac{1}{2}$ .

Suy ra $\frac{AD}{BC}=\frac{BD}{DC}=\frac{1}{2}$ hay $\frac{3}{BC}=\frac{4}{DC}=\frac{1}{2}$ .

Suy ra BC = 2 . 3 = 6 cm; DC = 4 . 2 = 8 cm.

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 33: Hai tam giác đồng dạng

Bài 34: Ba trường hợp đồng dạng của hai tam giác

Luyện tập chung (trang 91)

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng