Cho hình thang ABCD (AB // CD), biết góc ADB = góc DCB  (Hình 2a). Chứng minh rằng BD2 = AB.CD

Bài 10 trang 85 Toán 8 Tập 2: 

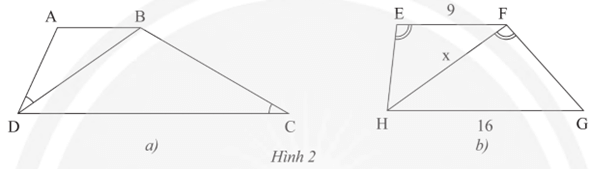
a) Cho hình thang ABCD (AB // CD), biết  $\widehat{\mathrm{ADB}}=\widehat{\mathrm{DCB}}$ (Hình 2a). Chứng minh rằng BD² = AB.CD.

b) Cho hình thang EFGH (EF // GH), $\widehat{\mathrm{HEF}}=\widehat{\mathrm{HFG}}$ , EF = 9 m, GH = 16 m (Hình 2b). Tính độ dài x của HF.

Trả lời

a) Xét ΔABD và ΔBDC có:

$\widehat{\mathrm{ADB}}=\widehat{\mathrm{DCB}}$ (gt)

$\widehat{\mathrm{ABD}}=\widehat{\mathrm{BDC}}$ (AB // CD, hai góc so le trong)

Do đso ΔABD ᔕ ΔBDC (g.g)

Suy ra $\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{BD}}{\mathrm{CD}}$  (các cạnh tương ứng).

Vậy BD² = AB.CD (đpcm).

b) Tương tự câu a, ta có: $\widehat{\mathrm{EHG}}=\widehat{\mathrm{FGH}}$

Xét tam giác EFH và FHG ta có:

$\widehat{\mathrm{EHG}}=\widehat{\mathrm{FGH}}$

$\widehat{\mathrm{HEF}}=\widehat{\mathrm{HFG}}$

Do đó ΔEFH ᔕ ΔFHG (g.g)

Suy ra $\frac{\mathrm{EF}}{\mathrm{HF}}=\frac{\mathrm{HF}}{\mathrm{GH}}$ (các cạnh tương ứng).

Khi đó HF² = EF.GH = 9.16 = 144 nên HF = 12 cm.

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8

Bài 1: Mô tả xác suất bằng tỉ số

Bài 2: Xác suất lí thuyết và xác suất thực nghiệm

Bài tập cuối chương 9