Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B

Bài 3 trang 113 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B’.

a) Chứng minh rằng EF // (BCC’B’).

b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF.

Trả lời

a)

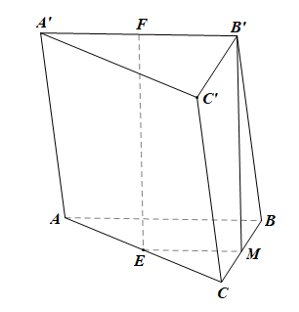
Gọi M là trung điểm của BC.

Trong mp(ABC), xét $∆$ABC có E, M lần lượt là trung điểm của AC, BC nên EM là đường trung bình của tam giác

Do đó EM // AB và EM = $\frac{1}{2}$ AB.

Mà AB // A’B’ nên EM // A’B’ hay EM // FB’.

Lại có AB = A’B’ và FB’ = $\frac{1}{2}$ A’B’ nên EM = FB’.

Trong mp(EMB’F), xét tứ giác EMB’F có EM // FB’ và EM = FB’ nên là hình bình hành.

Do đó EF // B’M, mà B’M ⊂ (BCC’B’) nên EF // (BCC’B’).

b)

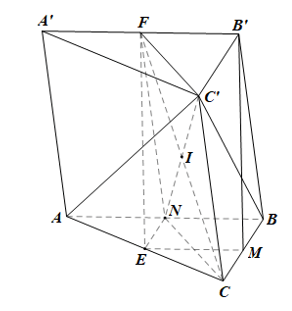
Gọi N là trung điểm của AB.

Trong mp(ABB’A’), xét hình bình hành ABB’A’ cũng là hình thang có N, F lần lượt là trung điểm của AB, A’B’ nên NF là đường trung bình của hình thang

Do đó NF // BB’ và $NF=\frac{A{A}^{\text{'}}+B{B}^{\text{'}}}{2}=\frac{2B{B}^{\text{'}}}{2}=B{B}^{\text{'}}$ .

Mà BB’ // CC’ nên NF // CC’.

Lại có BB’ = CC’ nên NF = CC’.

Trong mp(NFC’C), xét tứ giác NFC’C có NF // CC’ và NF = CC’ nên là hình bình hành.

Do đó hai đường chéo CF và NC’ cắt nhau tại trung điểm của mỗi đường.

Lại có NC’ ⊂ (ABC’) nên CF cắt (ABC’) tại trung điểm I của CF.

Vậy CF cắt (ABC’) tại trung điểm I của CF.