Cho hai mặt phẳng song song (P) và (P’). Trong mặt phẳng (P), cho đa giác A1A2
164
14/08/2023
Hoạt động 1 trang 110 Toán 11 Tập 1: Cho hai mặt phẳng song song (P) và (P’). Trong mặt phẳng (P), cho đa giác A1A2….An. Qua các đỉnh A1, A2, ..., An vẽ các đường thẳng song song với nhau và cắt mặt phẳng (P’) lần lượt tại A1’, A2’, ..., An’ (Hình 70 minh hoạ cho trường hợp n = 5).
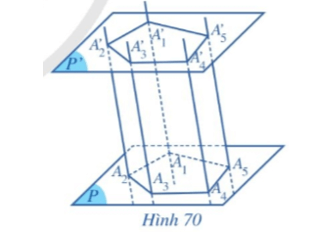
a) Các tứ giác A1A2A2’A1’, A2A3A3’A2’, …, AnA1A1’An’ là những hình gì?
b) Các cạnh tương ứng của hai đa giác A1A2…An và A1’A2’…An’ có đặc điểm gì?
Trả lời
a) Ta có: (P) // (P’);
(A1A2A2’A1’) ∩ (P) = A1A2;
(A1A2A2’A1’) ∩ (P’) = A1’A2’.
Do đó A1A2 // A1’A2’.
Trong mp (A1A2A2’A1’), tứ giác A1A2A2’A1’ có A1A1’ // A2A2’ và A1A2 // A1’A2’
Do đó A1A2A2’A1’ là hình bình hành.
Chứng minh tương tự ta có: các tứ giác A2A3A3’A2’, …, AnA1A1’An’ cũng là những hình bình hành.
Vậy các tứ giác A1A2A2’A1’, A2A3A3’A2’, …, AnA1A1’An’ là những hình bình hành.
b) Theo câu a, A1A2A2’A1’ là hình bình hành nên A1A2 = A1’A2’
Tương tự như vậy, ta kết luận các cạnh tương ứng của hai đa giác A1A2…An và A1’A2’…An’ có độ dài bằng nhau.

