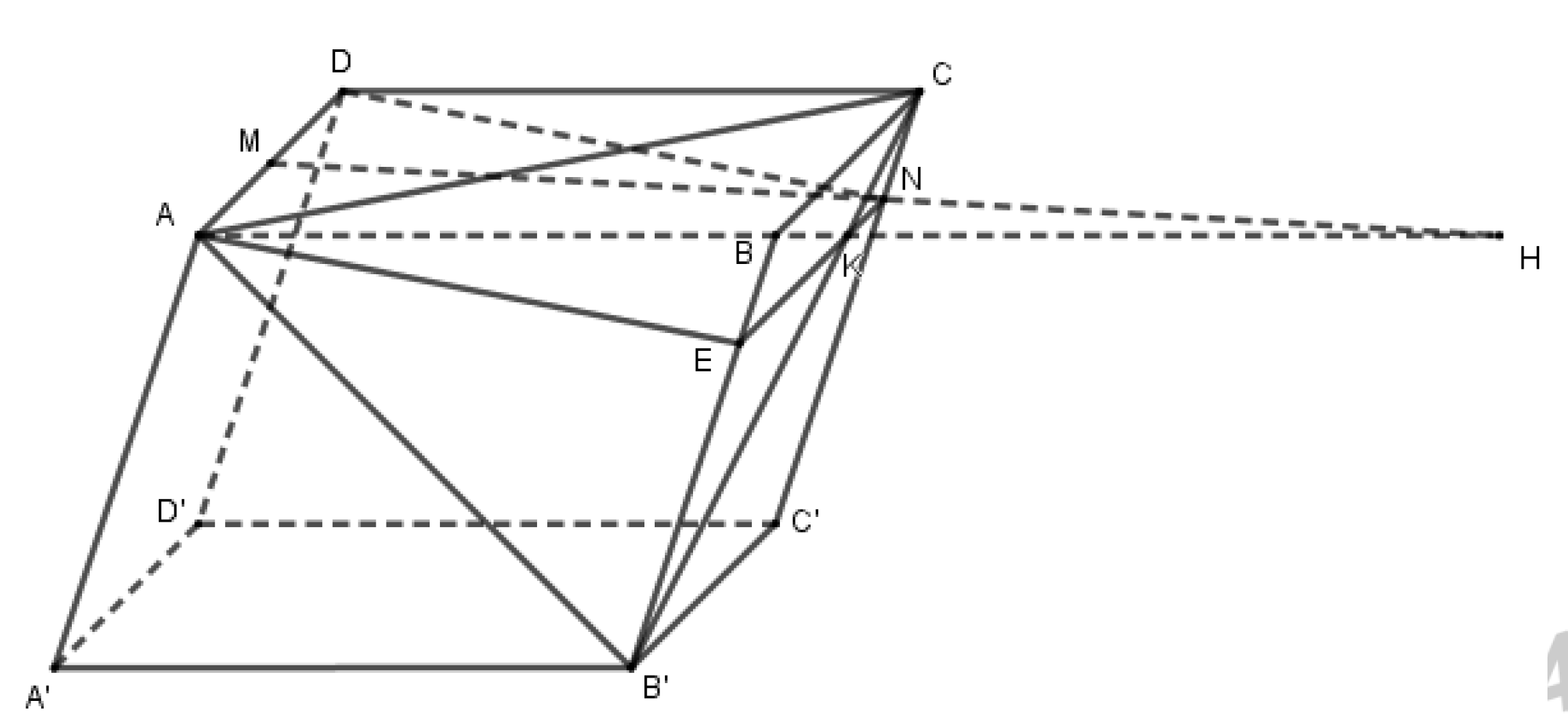
Cho hình hộp ABCD.A'B'C'D' (tham khảo hình vẽ). Hai điểm M, N lần lượt nằm trên hai cạnh AD, CC' sao cho AM = 1/2 AD, CN = 1/4CC'. Thiết diện của hình hộp cắt bởi mặt phẳng chứa đường thẳng M
33
24/04/2024
Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Hai điểm \(M,\,N\) lần lượt nằm trên hai cạnh \(AD,\,CC'\) sao cho \(AM = \frac{1}{2}AD,\,CN = \frac{1}{4}CC'\). Thiết diện của hình hộp cắt bởi mặt phẳng chứa đường thẳng \(MN\) và song song với mặt phẳng \(\left( {ACB'} \right)\) là
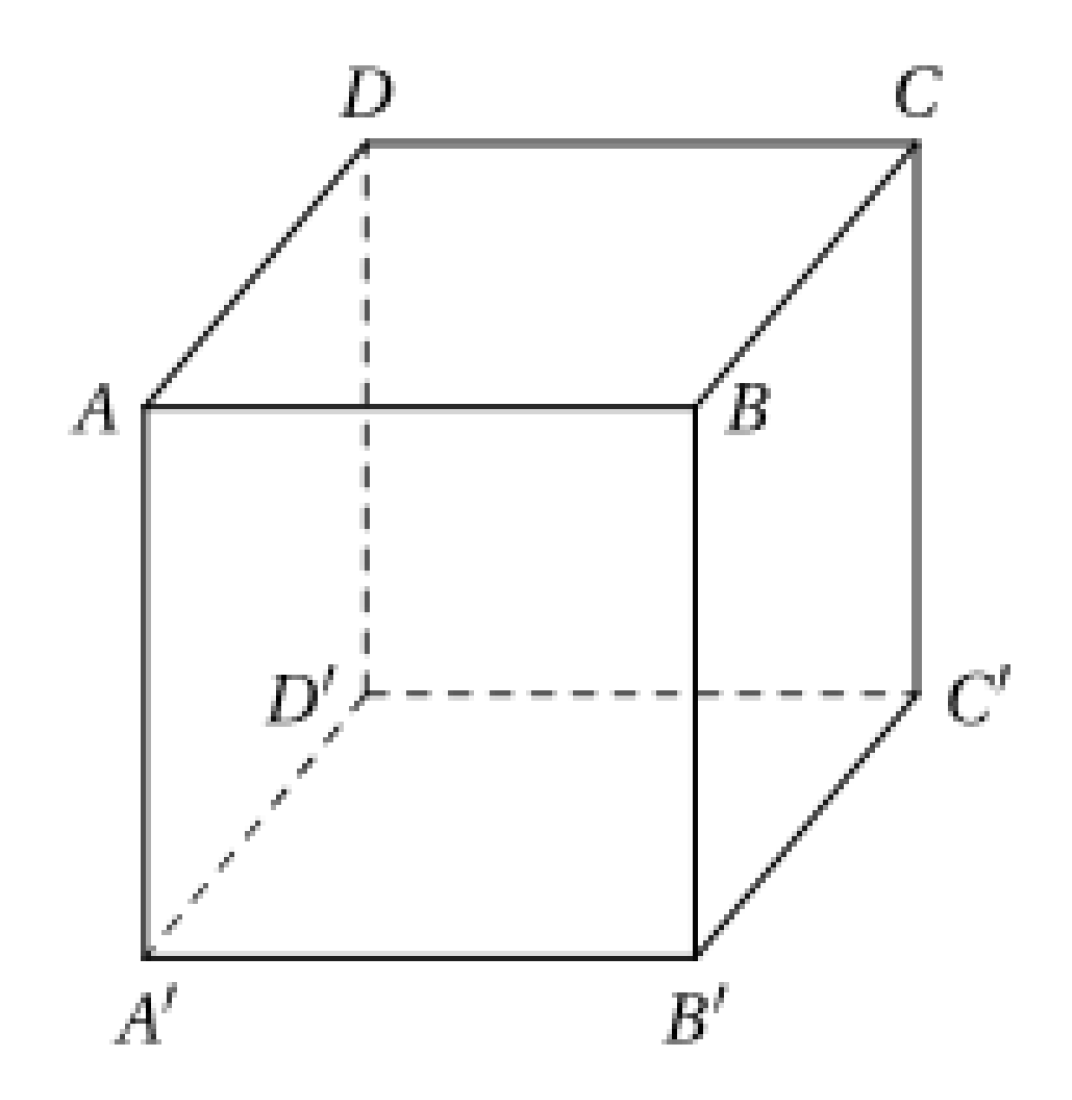
A. hình lục giác
B. hình ngũ giác
C. hình tam giác
D. không có thiết diện
Trả lời
Đáp án D
Phương pháp:
Chứng minh \(MN\) cắt mặt phẳng \(\left( {ACB'} \right)\) dẫn đến không có mặt phẳng cần tìm.
Cách giải:
Qua N kẻ \(NE//BC\) \(\left( {E \in BB'} \right)\), \(NE \cap B'C = K\).
Dễ thấy \(NE//BC//AD\) nên các điểm A, M, N, E cùng thuộc mặt phẳng \(\left( {ADNE} \right)\).
Lại có \(K = NE \cap CB' \Rightarrow K \in CB' \subset \left( {ACB'} \right) \Rightarrow AK \subset \left( {ACB'} \right)\)
Trong mặt phẳng \(\left( {ADMN} \right)\) gọi \(H = MN \cap AK \Rightarrow \left\{ \begin{array}{l}H \in MN\\H \in AK \subset \left( {ACB'} \right)\end{array} \right. \Rightarrow H = MN \cap \left( {ACB'} \right)\)
Do đó không có mặt phẳng nào chứa \(MN\) và song song \(\left( {ACB'} \right)\) .
Vậy không có thiết diện cần tìm.
