Phương pháp:
Gọi N là trung điểm của \(A'B'\), G là giao điểm của \(NC'\) với EF.
Từ đó mở rộng mặt phẳng \(\left( {FOE} \right)\) rồi tìm giao tuyến của \(\left( {FOE} \right)\) với các mặt của hình hộp.
Cách giải:
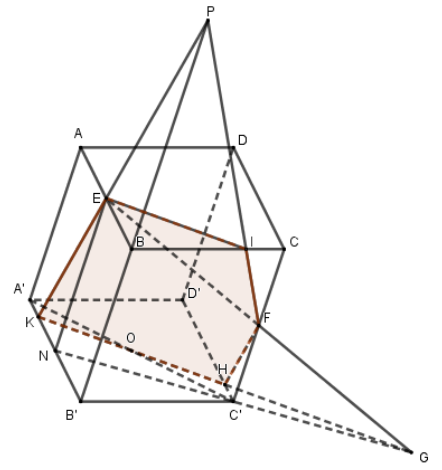
Gọi N là trung điểm của \(A'B' \Rightarrow NE//FC'\) nên bốn điểm N, E, F, C đồng phẳng.
Trong \(\left( {NEFC} \right)\), gọi \(G = NC' \cap EF \Rightarrow G \in EF \subset \left( {FOE} \right)\).
Trong \(\left( {A'B'C'D'} \right)\), gọi H, K lần lượt là giao điểm của GO với \(D'C'\), \(A'B'\)
Khi đó \(\left( {FOE} \right) \equiv \left( {GKE} \right)\).
Trong \(\left( {ABB'A'} \right)\), gọi \(P = KE \cap B'B \Rightarrow P \in BB' \subset \left( {BCC'B'} \right)\).
Trong \(\left( {BCC'B'} \right)\), gọi \(I = PF \cap BC \Rightarrow \left\{ \begin{array}{l}I \in BC\\I \in PF \subset \left( {GKE} \right) \equiv \left( {FOE} \right)\end{array} \right. \Rightarrow I = BC \cap \left( {FOE} \right)\).
Khi đó
\(\left( {FOE} \right) \cap \left( {A'B'C'D'} \right) = HK\)
\(\left( {FOE} \right) \cap \left( {ABB'A'} \right) = KE\)
\(\left( {FOE} \right) \cap \left( {ABCD} \right) = EI\)
\(\left( {FOE} \right) \cap \left( {BCC'B'} \right) = IF\)
\(\left( {FOE} \right) \cap \left( {DCC'D'} \right) = FH\)
Thiết diện là ngũ giác EIFHK.
Ta có, \(\frac{{IB}}{{IC}} = \frac{{PB}}{{CF}}\), \(CF = \frac{1}{2}CC' \Rightarrow \frac{{PB}}{{CF}} = \frac{{PB}}{{\frac{1}{2}CC'}} = 2.\frac{{PB}}{{BB'}}\) .
\(HC'//KN \Rightarrow \frac{{HC'}}{{KN}} = \frac{{GC'}}{{GN}}\)
Mà \(C'F//NE \Rightarrow \frac{{GC'}}{{GN}} = \frac{{C'F}}{{NE}} = \frac{1}{2} \Rightarrow \frac{{HC'}}{{KN}} = \frac{1}{2} \Rightarrow \frac{{A'K}}{{KN}} = \frac{1}{2} \Rightarrow \frac{{A'K}}{{A'N}} = \frac{1}{3} \Rightarrow \frac{{A'K}}{{A'B'}} = \frac{1}{6}\)
\( \Rightarrow \frac{{KN}}{{A'N}} = \frac{2}{3} = \frac{{K'N}}{{NB'}} \Rightarrow \frac{{K'N}}{{NB'}} = \frac{2}{5} \Rightarrow \frac{{NE}}{{PB'}} = \frac{2}{5} \Rightarrow \frac{{BB'}}{{PB'}} = \frac{2}{5} \Rightarrow \frac{{PB}}{{PB'}} = \frac{3}{5} \Rightarrow \frac{{PB}}{{BB'}} = \frac{3}{2}\)
Vậy \(\frac{{IB}}{{IC}} = \frac{{PB}}{{CF}} = 2.\frac{{PB}}{{BB'}} = 2.\frac{3}{2} = 3\).