Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình thoi cạnh a, AA’ ⊥ (ABCD), AA’ = 2a, AC = a. Tính khoảng cách

Bài 50 trang 110 SBT Toán 11 Tập 2: Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình thoi cạnh a, AA’ ⊥ (ABCD), AA’ = 2a, AC = a. Tính khoảng cách:

a) Từ điểm A đến mặt phẳng (BCC’B’);

b) Giữa hai mặt phẳng (ABB’A’) và (CDD’C’);

c*) Giữa hai đường thẳng BD và A’C.

Trả lời

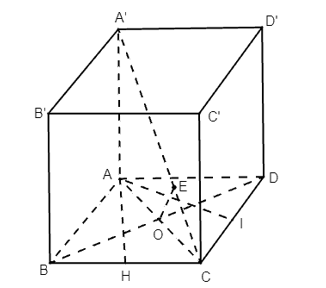
a) Gọi H là hình chiếu của A trên BC hay AH ⊥ BC.

Do ABCD.A’B’C’D là hình hộp nên AA’ // BB’.

Mà AA’ ⊥ (ABCD) nên BB’ ⊥ (ABCD).

Hơn nữa AH ⊂ (ABCD).

Từ đó ta có BB’ ⊥ AH.

Ta có: AH ⊥ BC, AH ⊥ BB’, BC ∩ BB’ = B trong (BCC’B’)

Suy ra AH ⊥ (BCC’B’).

Như vậy d(A, (BCC’B’)) = AH.

Xét tam giác ABC đều (do AB = BC = AC = a), AH là đường cao (do AH ⊥ BC)

Suy ra AH là đường trung tuyến nên ta có $BH=\frac{BC}{2}=\frac{a}{2}.$

Áp dụng định lí Pythagore trong tam giác ABH vuông tại H có:

AB² = AH² + BH²

Suy ra $AH=\sqrt{A{B}^2-B{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Vậy $d\left(A,\left(BC{C}^{\text{'}}{B}^{\text{'}}\right)\right)=AH=\frac{a\sqrt{3}}{2}.$

b) Do ABCD.A’B’C’D là hình hộp nên (ABB’A’) // (CDD’C’).

Như vậy: d((ABB’A’), (CDD’C’)) = d(A, (CDD’C’)).

Gọi I là hình chiếu của A trên CD hay AI ⊥ CD.

Do ABCD.A’B’C’D là hình hộp nên AA’ // DD’.

Mà AA’ ⊥ (ABCD) nên DD’ ⊥ (ABCD).

Hơn nữa AI ⊂ (ABCD).

Từ đó ta có DD’ ⊥ AI.

Ta có: AI ⊥ CD, AI ⊥ DD’, CD ∩ DD’ = D trong (CDD’C’)

Suy ra AI ⊥ (CDD’C’).

Khi đó: d(A, (CDD’C’)) = AI.

Xét tam giác ACD đều (do AC = AD = DC = a), AI là đường cao (do AI ⊥ CD)

Suy ra AI là đường trung tuyến nên ta có $ID=\frac{CD}{2}=\frac{a}{2}.$

Áp dụng định lí Pythagore trong tam giác ADI vuông tại I có:

AD² = AI² + DI²

Suy ra $AI=\sqrt{A{D}^2-D{I}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}.$

Vậy $d\left(\left(AB{B}^{\text{'}}{A}^{\text{'}}\right),\left(CD{D}^{\text{'}}{C}^{\text{'}}\right)\right)=AI=\frac{a\sqrt{3}}{2}.$

c) Gọi O là giao điểm của AC và BD.

Ta có ABCD là hình thoi nên AC ⊥ BD và $AO=\frac{AC}{2}=\frac{a}{2}.$

Do AA’ ⊥ (ABCD) và BD ⊂ (ABCD) nên AA’ ⊥ BD.

Ta có: BD ⊥ AA’, BD ⊥ AC, AA’ ∩ AC = A trong (AA’C)

Suy ra BD ⊥ (AA’C).

Gọi E là hình chiếu của O trên A’C hay OE ⊥ A’C.

Lại có: BD ⊥ (AA’C), OE ⊂ (AA’C).

Suy ra BD ⊥ OE.

Mà OE ⊥ A’C.

Từ đó ta có OE là đoạn vuông góc chung của hai đường thẳng BD và A’C.

Như vậy: d(BD, A’C) = OE.

Do AA’ ⊥ (ABCD) và AC ⊂ (ABCD) nên AA’ ⊥ AC.

Áp dụng định lí Pythagore trong tam giác A’AC vuông tại A ta có:

A'C² = A'A² + AC²

Suy ra $A^{\text{'}}C=\sqrt{A^{\text{'}}{A}^2+A{C}^2}=\sqrt{{\left(2a\right)}^2+a^2}=a\sqrt{5}.$

Xét tam giác CEO và tam giác CAA’ có:

$\widehat{OCE}$ chung

$\widehat{A^{\text{'}}AC}=\widehat{OEC}=90°$

Suy ra $\Delta CEO\backsim \Delta CA{A}^{\text{'}}\left(g.g\right)$

$\Rightarrow \frac{EO}{A{A}^{\text{'}}}=\frac{CO}{C{A}^{\text{'}}}\Rightarrow OE=\frac{A{A}^{\text{'}}.CO}{C{A}^{\text{'}}}.$

$\Rightarrow OE=\frac{2a.\frac{a}{2}}{a\sqrt{5}}=\frac{a\sqrt{5}}{5}.$

Vậy $d\left(BD.A^{\text{'}}C\right)=OE=\frac{a\sqrt{5}}{5}.$

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 4: Hai mặt phẳng vuông góc

Bài 5: Khoảng cách

Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Bài tập cuối chương 8