Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a. Tính khoảng cách: Từ điểm C đến mặt phẳng (SAB); Giữa hai đường thẳng SA và BC

Bài 47 trang 110 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB ⊥ BC, SA = AB = 3a, BC = 4a. Tính khoảng cách:

a) Từ điểm C đến mặt phẳng (SAB);

b) Giữa hai đường thẳng SA và BC;

c) Từ điểm A đến mặt phẳng (SBC);

d) Từ điểm B đến mặt phẳng (SAC);

e*) Giữa hai đường thẳng AB và SC.

Trả lời

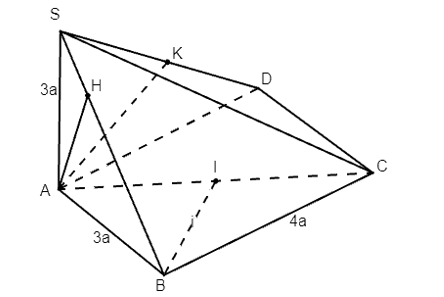
a) Do SA ⊥ (ABC), BC ⊂ (ABC) nên SA ⊥ BC.

Ta có: BC ⊥ SA, BC ⊥ AB và SA ∩ AB = A trong (SAB)

Suy ra BC ⊥ (SAB).

Như vậy: d(C, (SAB)) = BC = 4a.

b) Do SA ⊥ (ABC), AB ⊂ (ABC) nên SA ⊥ AB.

Mặt khác AB ⊥ BC.

Suy ra AB là đoạn vuông góc chung của hai đường thẳng SA và BC.

Như vậy: d(SA, BC) = AB = 3a.

c) Gọi H là hình chiếu của điểm A trên SB hay AH ⊥ SB.

Do BC ⊥ (SAB), AH ⊂ (SAB) nên BC ⊥ AH.

Ta có: AH ⊥ BC, AH ⊥ SB và BC ∩ SB = B trong (SBC)

Suy ra AH ⊥ (SBC).

Như vậy: d(A, (SBC)) = AH.

Áp dụng hệ thức lượng trong tam giác SAB vuông tại A (SA ⊥ AB), đường cao AH ta có:

$\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{B}^2}=\frac{1}{{\left(3a\right)}^2}+\frac{1}{{\left(3a\right)}^2}=\frac{2}{9a^2}.$

$\Rightarrow AH=\frac{3\sqrt{2}a}{2}.$

Vậy $d\left(A,\left(SBC\right)\right)=AH=\frac{3\sqrt{2}a}{2}.$

d) Gọi I là hình chiếu của B trên AC hay BI ⊥ AC.

Do SA ⊥ (ABC), BI ⊂ (ABC) nên SA ⊥ BI.

Ta có: BI ⊥ AC, BI ⊥ SA, AC ∩ SA = A trong (SAC)

Suy ra BI ⊥ (SAC).

Như vậy: d(B, (SAC)) = BI.

Áp dụng hệ thức lượng trong tam giác ABC vuông tại B (AB ⊥ BC), đường cao BI ta có:

$\frac{1}{B{I}^2}=\frac{1}{A{B}^2}+\frac{1}{B{C}^2}=\frac{1}{{\left(3a\right)}^2}+\frac{1}{{\left(4a\right)}^2}=\frac{25}{144a^2}.$

$\Rightarrow BI=\frac{12a}{5}.$

Vậy $d\left(B,\left(SAC\right)\right)=BI=\frac{12a}{5}.$

e*) · Lấy D ∈ (ABC) sao cho ABCD là hình bình hành.

Mà $\widehat{ABC}=90°$ (do AB ⊥ BC) nên ABCD là hình chữ nhật.

Suy ra CD ⊥ AD.

Do SA ⊥ (ABC), CD ⊂ (ABC) nên SA ⊥ CD.

Ta có: CD ⊥ AD, CD ⊥ SA, AD ∩ SA = A trong (SAD)

Suy ra CD ⊥ (SAD).

· Gọi K là hình chiếu của A trên SD hay AK ⊥ SD.

Do CD ⊥ (SAD), AK ⊂ (SAD) nên CD ⊥ AK.

Ta có: AK ⊥ SD, AK ⊥ CD, SD ⋂ CD = D trong (SCD)

Suy ra AK ⊥ (SCD).

Ta có: AB // CD (vì ABCD là hình chữ nhật) và CD ⊂ (SCD).

Suy ra AB // (SCD).

Như vậy: d(AB, SC) = d(AB, (SCD)) = d(A, (SCD)) = AK.

Ta có: SA ⊥ (ABC), AD ⊂ (ABC) nên SA ⊥ AD hay

Do ABCD là hình chữ nhật nên AD = BC = 4a.

Áp dụng hệ thức lượng trong tam giác SAD vuông tại A đường cao AK ta có:

$\frac{1}{A{K}^2}=\frac{1}{S{A}^2}+\frac{1}{S{D}^2}=\frac{1}{{\left(3a\right)}^2}+\frac{1}{{\left(4a\right)}^2}=\frac{25}{144a^2}.$

$\Rightarrow AK=\frac{12a}{5}.$

Vậy $d\left(AB,SC\right)=AK=\frac{12a}{5}.$

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 4: Hai mặt phẳng vuông góc

Bài 5: Khoảng cách

Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Bài tập cuối chương 8