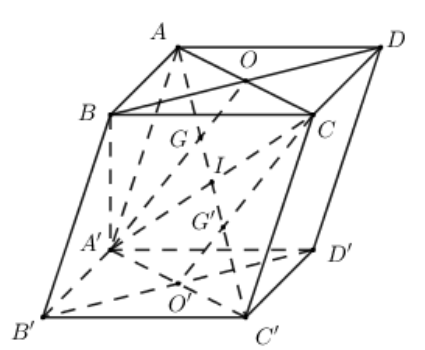
Cho hình hộp ABCD.A',B',C',D'. Gọi G và G’ là trọng tâm các tam giác BDA' và A'CC'. Khẳng định nào sau đây đúng? A. GG' = 3/2AC' B. GG' = AC' C. GG' = 1/2}AC' D. GG' = 1/3AC'
Cho hình hộp \[ABCD.A',B',C',D'\]. Gọi G và G’ là trọng tâm các tam giác \[BDA'\] và \[A'CC'\].
Khẳng định nào sau đây đúng?
A. \[GG' = \frac{3}{2}AC'\]
B. \[GG' = AC'\]
C. \[GG' = \frac{1}{2}AC'\]
D. \[GG' = \frac{1}{3}AC'\]