Cho hình chóp S.ABCD với đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo, tam giác SBD là tam giác đều

Thực hành 2 trang 116 Toán 11 Tập 1: Cho hình chóp S.ABCD với đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo, tam giác SBD là tam giác đều. Một mặt phẳng (α) di động song song với mặt phẳng (SBD) và cắt đoạn thằng AC. Chứng minh các giao tuyến của (α) với hình chóp tạo thành một tam giác đều.

Trả lời

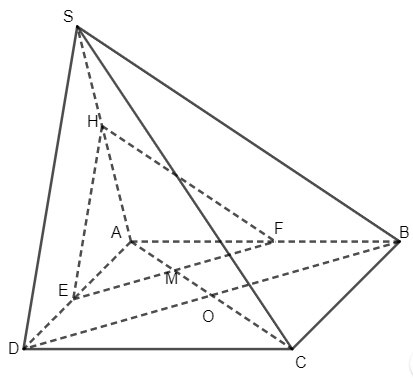
+) Gọi M là giao điểm của mặt phẳng (α) với AC.

Trong mặt phẳng (ABCD), từ điểm M kẻ đường thẳng song song với BD cắt AD và AB tại E và F.

Trong mặt phẳng (SAB), từ điểm F kẻ đường thẳng song song với SB cắt SA tại H.

Trong mặt phẳng (SAD), nối điểm E và H ta được mặt phặng (EFH) chính là mặt phẳng (α) cần dựng.

+) Xét tam giác ABD, có: EF // BD nên $\frac{EF}{BD}=\frac{AE}{AD}=\frac{AF}{AB}$ (định lí Thales).

Xét tam giác SAB, có: FH // SB nên $\frac{FH}{SB}=\frac{AF}{AB}=\frac{AH}{SA}$ (định lí Thales).

Xét tam giác SAD, có: EH // SD nên $\frac{EH}{SD}=\frac{AH}{SA}=\frac{AE}{AD}$ (định lí Thales).

Suy ra $\frac{EF}{BD}=\frac{FH}{SB}=\frac{EH}{SD}$

Mà tam giác SBD là tam giác đều nên BD = SB = SD.

Do đó EF = FH = EH. Vì vậy giao tuyến của (α) với hình chóp SABCD là hình tam giác đều.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hai đường thẳng song song

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Phép chiếu song song

Bài tập cuối chương 4

Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm