Bài 2 trang 120 Toán 11 Tập 1: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo. Gọi M, N lần lượt là trung điểm của SA, SD.
a) Chứng minh rằng (OMN) // (SBC).
b) Gọi E là trung điểm của AB và F là một điểm thuộc ON. Chứng minh EF song song với (SBC).
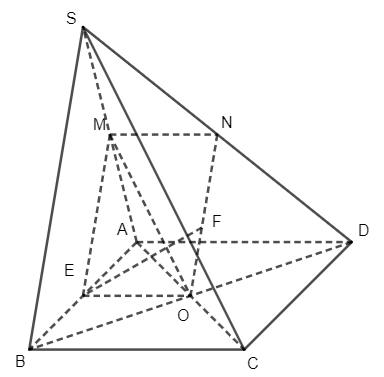
a) +) Trong tam giác SAD có: MN // AD (đường trung bình) mà AD // BC nên MN // BC.
Mặt khác BC ⊂ (SBC)
Suy ra MN // (SBC).
+) Trong tam giác SAC, có: OM // SC (đường trung bình) mà SC ⊂ (SBC) nên OM // (SBC).
+) Ta lại có MN, OM ⊂ (OMN) và OM cắt MN tại M
Vì vậy (OMN) // (SBC).
b) +) Trong tam giác SAB, có: EM // SB (đường trung bình) mà SB ⊂ (SBC) nên EM // (SBC).
Từ điểm M ta xác định được duy nhất một mặt phẳng song song với (SBC) nên EM ⊂ (OMN).
Do đó EF ⊂ (OMN) mà (OMN) // (SBC) nên EF // (SBC).
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Hai đường thẳng song song
Bài 3: Đường thẳng và mặt phẳng song song