Cho hình chóp S.ABCD. Gọi G, E lần lượt là trọng tâm các tam giác SAD và SCD. Lấy M, N lần lượt là trung điểm AB, BC. Khẳng định nào sau đây đúng? A. GE cắt BC B. GE và MN chéo nhau
Cho hình chóp \(S.ABCD\). Gọi G, E lần lượt là trọng tâm các tam giác SAD và SCD. Lấy M, N lần lượt là trung điểm AB, BC. Khẳng định nào sau đây đúng?
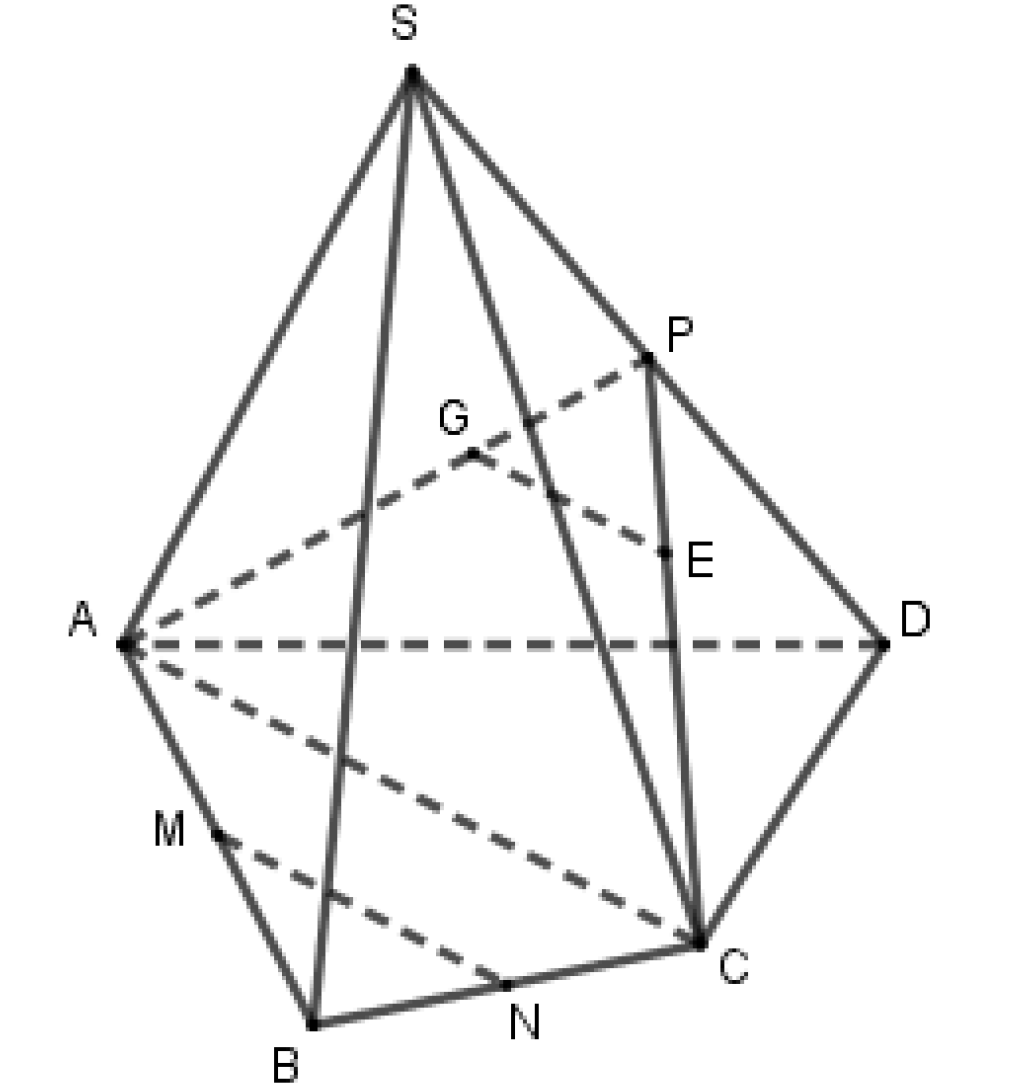
A. \(GE\) cắt \(BC\)
B. \(GE\) và \(MN\) chéo nhau
C. \(DE//MN\)
D. \(MN//SD\)
