Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, SC, OB. Gọi Q là giao điểm của SD với mp ( MNP). Tính SQ/SD A. SQ/SD = 1/4 B. SQ/SD = 1/3 C.
56
23/04/2024
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, SC, OB. Gọi Q là giao điểm của SD với mp (MNP). Tính SQSD.
A. SQSD=14.
B. SQSD=13.
C. SQSD=15.
D. SQSD=625.
Trả lời
Đáp án A
Phương pháp:
Tìm điểm Q.
Sử dụng định lí Menelaus để tính tỉ số.
Cách giải:
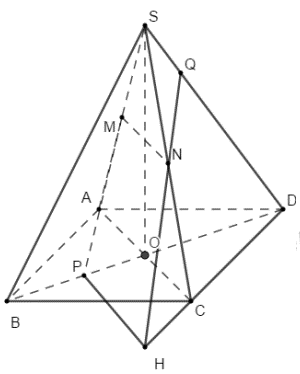
Trong (ABCD) lấy PH||MN(H∈CD)
Trong (SCD) gọi Q=NH∩SD
Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến QNH ta có: HDHC.NCNS.QSQD=1
Mà N là trung điểm của SC ⇒NCNS=1.
Mặt khác áp dụng định lí Ta-lét trong tam giác DPH ta có HDHC=DPOP=3 (vì P là trung điểm của OB).
Do đó ta có QSQD=13⇒SQSD=14

