Đáp án C

Phương pháp:

+ Xác định điểm I.

+ Xác định thiết diện.

+ Sử dụng công thức He-rong để tính diện tích tam giác: \[{S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \].

Cách giải:

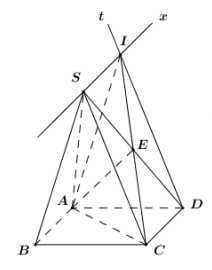
Trong \[\left( {SCD} \right)\] kẻ \[Dt\parallel SC\]

Ta có \[\left\{ \begin{array}{l}S \in \left( {SAB} \right) \cap \left( {SCD} \right)\\\left( {SAB} \right) \supset AB,\left( {SCD} \right) \supset CD\\AB\parallel CD\left( {gt} \right)\end{array} \right. \Rightarrow \] Giao tuyến của \[\left( {SAB} \right),\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD. Trong \[\left( {SAB} \right)\] kẻ \[Sx\parallel AB \Rightarrow \left( {SAB} \right) \cap \left( {SCD} \right) = Sx\]

Trong \[\left( {SCD} \right)\] gọi \[I = Dt \cap Sx\] ta có: \[\left\{ \begin{array}{l}I \in Dt\\I \in Sx \subset \left( {SAB} \right) \Rightarrow I \in \left( {SAB} \right)\end{array} \right. \Rightarrow I = Dt \cap \left( {SAB} \right)\].

Trong \[\left( {SCD} \right)\] gọi \[E = CI \cap SD\], khi đó thiết diện của chóp cắt bởi \[\left( {AIC} \right)\] là tam giác AEC.

ABCD là hình vuông cạnh \[a \Rightarrow AC = a\sqrt 2 \].

Dễ dàng chứng minh được SBAI, SCDI là hình bình hành \[ \Rightarrow AI = SB = a,E\] là trung điểm của SD, IC.

Tam giác SAD có \[SA = AD = a,\angle SAD = 90^\circ \Rightarrow \Delta SAD\] vuông cân tại \[A \Rightarrow SD = SA\sqrt 2 = a\sqrt 2 \].

\[ \Rightarrow AE = \frac{1}{2}SD = \frac{{a\sqrt 2 }}{2}\]

Xét tam giác IAC có:

\[A{E^2} = \frac{{A{I^2} + A{C^2}}}{2} - \frac{{I{C^2}}}{4} \Leftrightarrow \frac{{{a^2}}}{2} = \frac{{{a^2} + 2{a^2}}}{2} - \frac{{I{C^2}}}{4}\]

\[ \Rightarrow \frac{{I{C^2}}}{4} = {a^2} \Leftrightarrow I{C^2} = 4{a^2} \Leftrightarrow IC = 2a \Rightarrow EC = \frac{1}{2}IC = a\]

Khi đó áp dụng công thức Hê-rông ta có: \[{S_{\Delta AEC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \frac{{{a^2}\sqrt 7 }}{8}\]