Cho hình chóp $S.ABCD$ có đáy là hình thang, $AD$ là đáy lớn thỏa mãn $AD = 2BC$. Các điểm $M,N$ lần lượt là trung điểm của các cạnh $SA,\,\,SD$.

     a) Chứng minh đường thẳng $MN$ song song với mặt phẳng $\left( {SBC} \right)$.

     b) Mặt phẳng $\left( {MCD} \right)$ cắt $SB$ tại $E$. Tính tỉ số $\frac{{SE}}{{EB}}$.

Phương pháp:

a) $\left\{ \begin{array}{l}a||b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a||\left( P \right)$.

b) Chọn $SB \subset \left( Q \right)$, tìm $d = \left( Q \right) \cap \left( {MCD} \right)$, từ đó suy ra $E = d \cap SB$.

     Sử dụng tính chất trọng tâm và định lí Ta-lét.

Cách giải:

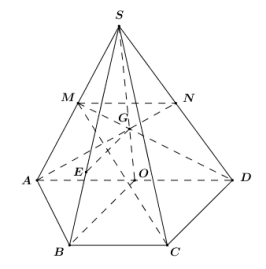
a) Vì $MN$ là đường trung bình của tam giác $SAD \Rightarrow MN||AD$ (tính chất đường trung bình).

Mà $AD||BC\left( {gt} \right) \Rightarrow MN||BC$.

Lại có $BC \cap \left( {SBC} \right) \Rightarrow MN||\left( {SBC} \right)$.

b) Gọi $O$ là trung điểm của $AD$ ta có: $\left\{ \begin{array}{l}OD = BC = \frac{1}{2}AD\\OD||BC\left( {AD||BC} \right)\end{array} \right. \Rightarrow BCDO$ là hình bình hành $\Rightarrow BO||CD$.

Chọn $SB \subset \left( {SBO} \right)$, tìm giao tuyến của $\left( {MCD} \right)$ và $\left( {SBO} \right)$.

+ $G$ là điểm chung thứ nhất.

$\left\{ \begin{array}{l}\left( {SBO} \right) \supset BO\\\left( {MCD} \right) \supset CD\\BO||CD\left( {cmt} \right)\end{array} \right.$ Þ Giao tuyến của $\left( {MCD} \right)$ và $\left( {SBO} \right)$ là đường thẳng qua $G$ và song song với $BO,CD$.

Trong $\left( {SBO} \right)$ kẻ $GE||BO\left( {E \in SB} \right) \Rightarrow \left( {MCD} \right) \cap \left( {SBO} \right) = GE$.

Ta có: $\left\{ \begin{array}{l}E \in SB\\E \in GH \subset \left( {MCD} \right)\end{array} \right. \Rightarrow E = SB \cap \left( {MCD} \right)$.

Xét tam giác $SAD$ có $G$ là giao điểm của hai đường trung tuyến

Þ $G$ là trọng tâm tam giác $SAD \Rightarrow \frac{{SG}}{{GO}} = 2$.

Do $GE||OB$ nên áp dụng đinh lí Ta-lét ta có $\frac{{SE}}{{EB}} = \frac{{SG}}{{GO}} = 2$.