Đáp án B

Phương pháp:

Dựng các đường thẳng qua $M$ và song song với các cạnh của tam giác $SAB$ ta được mặt phẳng $\left( \alpha \right)$ cần dựng

Từ đó ta xác định thiết diện của hình chóp cắt bởi mặt phẳng $\left( \alpha \right)$

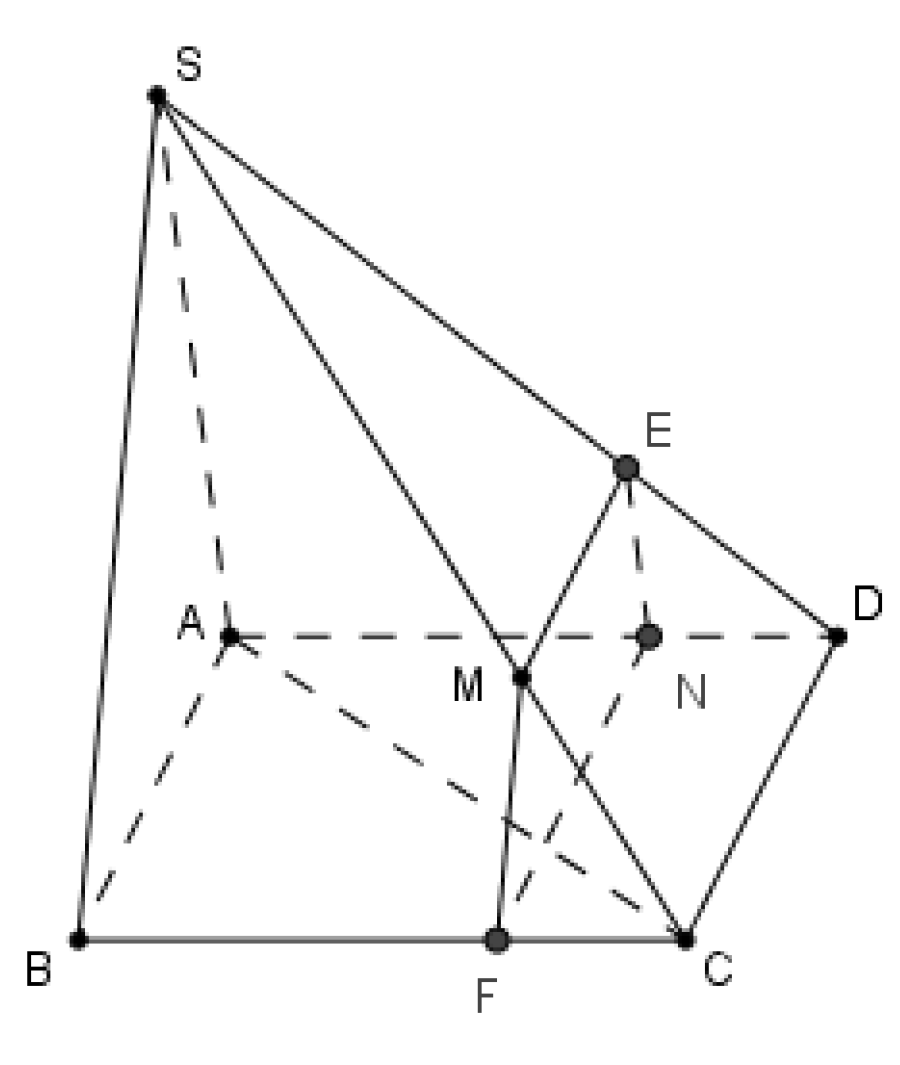
Cách giải:

+ Trong mặt phẳng $\left( {SBC} \right)$ kẻ $MF//SB$ $\left( {F \in BC} \right)$

+ Trong mặt phẳng $\left( {ABCD} \right)$ kẻ $FN//BA$ $\left( {N \in AD} \right)$

Từ đó ta có $\left( {MNF} \right)//\left( {SAB} \right)$

Trong $\left( {SCD} \right)$ kẻ $ME//CD$ $\left( {E \in SD} \right) \Rightarrow ME//CD//FN//AB$ hay $\left( {MNF} \right) \equiv \left( {MFNE} \right)$

Suy ra $\left( \alpha \right) \equiv \left( {MFNE} \right)$

Ta có $\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = MF\\\left( \alpha \right) \cap \left( {SDC} \right) = ME\\\left( \alpha \right) \cap \left( {SAD} \right) = NE\\\left( \alpha \right) \cap \left( {ABCD} \right) = NF\end{array} \right.$ nên thiết diện cắt bởi $\left( \alpha \right)$là tứ giác $MENF$

Mà $ME//FN \Rightarrow MENF$ là hình thang.