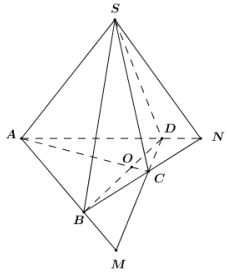
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi O là giao điểm của AC và BD, M là giao điểm của AB và CD, N là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng ( SAB ) và ( SCD) là?
36
23/04/2024
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi O là giao điểm của AC và BD, M là giao điểm của AB và CD, N là giao điểm của AD và BC. Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\) là?
A. SA
B. SN
C. SM
D. SO
Trả lời
Đáp án C
Phương pháp:
Xác định hai điểm chung của hai mặt phẳng.
Cách giải:
Xét \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\) có:
+ S là điểm chung thứ nhất.
+ \(M = AB \cap C{\rm{D}} \Rightarrow \left\{ \begin{array}{l}M \in {\rm{A}}B \subset \left( {SAB} \right) \Rightarrow M \in \left( {SAB} \right)\\M \in C{\rm{D}} \subset \left( {SC{\rm{D}}} \right) \Rightarrow M \in \left( {SC{\rm{D}}} \right)\end{array} \right.\)
\( \Rightarrow M \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) \Rightarrow \) M là điểm chung thứ hai.
Vậy \(\left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right) = SM\).