Phương pháp:
a) Xác định giao tuyến dựa vào yếu tố song song.
b) Chọn \[SC \subset \left( {SAC} \right),\] xác định giao tuyến \[\Delta = \left( {AMN} \right) \cap \left( {SAC} \right).\] Khi đó giao điểm của SC và \[\left( {AMN} \right)\] chính là giao điểm của SC và \[\Delta .\]
c) \[d||a \subset \left( P \right) \Rightarrow d||\left( P \right).\]
Cách giải:
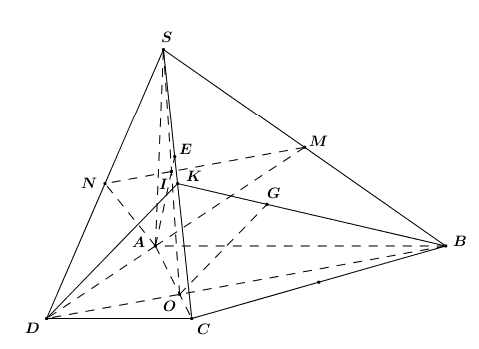
a) Xét \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] có:
+ S là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}\left( {SAB} \right) \supset AB\\\left( {SCD} \right) \supset CD\\AB||CD{\rm{ }}\left( {gt} \right)\end{array} \right. \Rightarrow \]Giao tuyến của \[\left( {SAB} \right),{\rm{ }}\left( {SCD} \right)\] là đường thẳng đi qua S và song song với AB, CD.
Trong \[\left( {SAB} \right)\] kẻ đường thẳng d đi qua S và \[d||AB||CD.\]
Vậy \[d = \left( {SAB} \right) \cap \left( {SCD} \right).\]
b) Chọn \[SC \subset \left( {SAC} \right),\] tìm giao tuyến của \[\left( {SAC} \right)\] và \[\left( {AMN} \right).\]
+ A là điểm chung thứ nhất.
+ Trong \[\left( {SBD} \right)\] gọi \[I = MN \cap SO\] ta có: \[I \in SO \subset \left( {SAC} \right) \Rightarrow I \in \left( {SAC} \right).\]
Trong \[\left( {SAC} \right)\] gọi \[E = AI \cap SC\] ta có:
\[\left\{ \begin{array}{l}E \in AI \subset \left( {AMN} \right) \Rightarrow E \in \left( {AMN} \right)\\E \in SC\end{array} \right. \Rightarrow E = SC \cap \left( {AMN} \right).\]
c) Gọi K là trung điểm của SC.
Vì G là trọng tâm tam giác SBC \[ \Rightarrow G \in BK\] và \[\frac{{BG}}{{BK}} = \frac{2}{3}\] (Tính chất trọng tâm).
Do \[AB||CD{\rm{ }}\left( {gt} \right),\] áp dụng định lí Ta-lét ta có: \[\frac{{BO}}{{OD}} = \frac{{AB}}{{CD}} = 2 \Rightarrow \frac{{BO}}{{BD}} = \frac{2}{3}.\]
\[ \Rightarrow \frac{{BG}}{{BK}} = \frac{{BO}}{{BD}} = \frac{2}{3} \Rightarrow OG||DK\] (Định lí Ta-lét đảo).
Mà \[DK \subset \left( {SCD} \right).\] Vậy \[OG||\left( {SCD} \right).\]

