Bài 2 trang 133 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và O là giao điểm của AC và BD. Gọi M, N, P lần lượt là ba điểm nằm trên các cạnh AB, BC, SO. Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình chóp S.ABCD (nếu có).
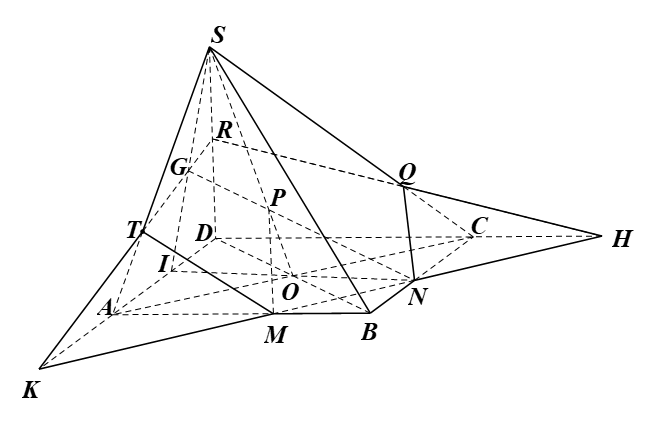
• Do M ∈ AB, N ∈ BC và AB ⊂ (ABCD), BC ⊂ (ABCD) nên MN ⊂ (ABCD)
Mà MN ⊂ (MNP)
Suy ra (MNP) ∩ (ABCD) = MN.
• Trong mặt phẳng (ABCD), gọi H là giao điểm của MN và DC; K là giao điểm của MN và AD; I là giao điểm của NO và AD.
Trong mặt phẳng (SIO), gọi G là giao điểm của NP và SI.
Trong mặt phẳng (SAD), gọi T là giao điểm của KG và SA và R là giao điểm của KG và SD.
Trong mặt phẳng (SDC), gọi Q là giao điểm của RH và SC.
Khi đó, (MNP) ∩ (SAB) = TM.
(MNP) ∩ (SBC) = NQ;
(MNP) ∩ (SDC) = QR;
(MNP) ∩ (SAD) = RT.
Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: