Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là trọng tâm của tam giác SAD. Lấy điểm M thuộc cạnh AB sao cho AB = 3AM

Trả lời

Phương pháp:

a) Sử dụng định lí ba giao tuyến song song: $\left\{ \begin{array}{l}\left( \alpha \right) \cap \left( \beta \right) = {d_1}\\\left( \beta \right) \cap \left( \gamma \right) = {d_2}\\\left( \alpha \right) \cap \left( \gamma \right) = {d_3}\\{d_1}//{d_2}\end{array} \right. \Rightarrow {d_3}//{d_1}//{d_2}$.

Cách giải:

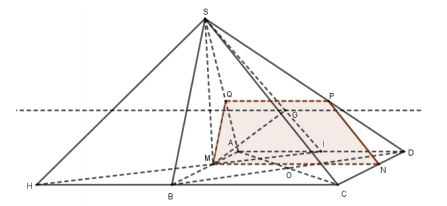
1) Tìm giao tuyến của mặt phẳng $\left( {SAD} \right)$ và mặt phẳng $\left( {GBC} \right)$. Tìm giao điểm $H$ của đường thẳng $BC$ với mặt phẳng $\left( {SGM} \right)$.

Dễ thấy $G \in \left( {GBC} \right) \cap \left( {SAD} \right)$.

Xét các mặt phẳng: $\left( {GBC} \right),{\rm{ }}\left( {SAD} \right),{\rm{ }}\left( {ABCD} \right)$ có:

$\left\{ \begin{array}{l}\left( {GBC} \right) \cap \left( {SAD} \right) = Gx\\\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\\\left( {ABCD} \right) \cap \left( {GBC} \right) = BC\\BC//AD\end{array} \right. \Rightarrow Gx//AB//CD$

Vậy $\left( {SAD} \right) \cap \left( {GBC} \right) = Gx$ là đường thẳng đi qua $G$ và song song $AD$.

Gọi $I$ là trung điểm $AD$, khi đó $\left( {SGM} \right) \equiv \left( {SIM} \right)$.

Trong $\left( {ABCD} \right)$, gọi $H = IM \cap BC \Rightarrow \left\{ \begin{array}{l}H \in IM \subset \left( {SIM} \right)\\H \in BC\end{array} \right. \Rightarrow H = BC \cap \left( {SMG} \right)$.