Phương pháp:
a, b) Xác định 2 điểm chung của hai mặt phẳng.
c) Sử dụng định lí Ta-lét.
Cách giải:
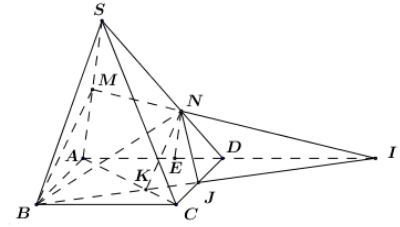
a) Xét \[\left( {BMN} \right)\] và \[\left( {ABCD} \right)\] có:
+ B là điểm chung thứ nhất.
+ \[\left\{ \begin{array}{l}I \in MN \subset \left( {BMN} \right) \Rightarrow I \in \left( {BMN} \right)\\I \in AD \subset \left( {ABCD} \right) \Rightarrow I \in \left( {ABCD} \right)\end{array} \right. \Rightarrow I \in \left( {BMN} \right) \cap \left( {ABCD} \right) \Rightarrow I\] là điểm chung thứ hai.
Vậy \[\left( {BMN} \right) \cap \left( {ABCD} \right) = BI\]
b) Xét \[\left( {BMN} \right)\] và \[\left( {SCD} \right)\] có:
+ N là điểm chung thứ nhất.
+ \[J = BI \cap CD \Rightarrow \left\{ \begin{array}{l}J \in BI \subset \left( {BMN} \right) \Rightarrow J \in \left( {BMN} \right)\\J \in CD \subset \left( {SCD} \right) \Rightarrow J \in \left( {SCD} \right)\end{array} \right. \Rightarrow J \in \left( {BMN} \right) \cap \left( {SCD} \right) \Rightarrow J\] là điểm chung thứ hai.
Vậy \[\left( {BMN} \right) \cap \left( {SCD} \right) = NJ\]. Từ đó ta có thiết diện của hình chóp cắt bởi \[\left( {BMN} \right)\] là tứ giác BMNJ.
c) Trong \[\left( {SAD} \right)\] kẻ \[NE\parallel SA\left( {E \in AD} \right)\] ta có: \[\frac{{NE}}{{SA}} = \frac{{DN}}{{SD}} = \frac{1}{3} \Rightarrow \frac{{NE}}{{2MA}} = \frac{1}{3} \Leftrightarrow \frac{{NE}}{{MA}} = \frac{2}{3}\].
Mà \[\frac{{NE}}{{MA}} = \frac{{IN}}{{IM}} \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3} \Rightarrow \frac{{NI}}{{MN}} = 2\]
Mà IM là trung tuyến của tam giác \[SAI \Rightarrow N\] là trọng tâm tam giác SAI.
\[ \Rightarrow D\] là trung điểm của \[AI \Rightarrow \frac{{ID}}{{IA}} = \frac{1}{2} = \frac{{DJ}}{{AB}} = \frac{{DJ}}{{CD}} \Rightarrow J\] là trung điểm của CD.
\[ \Rightarrow \frac{{CJ}}{{AB}} = \frac{1}{2} = \frac{{KJ}}{{KB}} \Rightarrow KJ = \frac{1}{2}KB \Rightarrow IK = KJ + IJ = \frac{1}{2}KB + \frac{3}{2}KB = 2KB\]
Vậy \[\frac{{IN}}{{MN}} = \frac{{IK}}{{BK}} = 2 \Rightarrow BM\parallel KN\] (đpcm).

