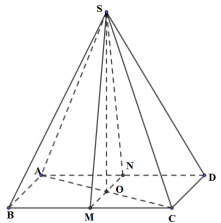
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là đường thẳng nào: A. SD. B. SO (O là tâm
35
24/04/2024
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là đường thẳng nào:
A. SD.
B. SO (O là tâm hình bình hành ABCD).
C. SG (G là trung điểm của AB).
D. SF (F là trung điểm của CD).
Trả lời
Đáp án B
Phương pháp:
Xác định 2 điểm phân biệt cùng thuộc cả hai mặt phẳng. Từ đó kết luận giao tuyến.
Cách giải:
Gọi O là tâm của hình bình hành ABCD Þ O là trung điểm của AC.
Ta có:
ON là đường trung bình của \(\Delta AC{\rm{D}} \Rightarrow ON//C{\rm{D}}\)
OM là đường trung bình của \(\Delta ABC \Rightarrow OM//AB\)
Mà \(AB//C{\rm{D}} \Rightarrow OM//C{\rm{D}} \Rightarrow \) O, M, N thẳng hàng
\( \Rightarrow {\rm{AC}} \cap {\rm{MN = O}} \Rightarrow {\rm{O}} \in \left( {SAC} \right) \cap \left( {SMN} \right)\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SMN} \right) \Rightarrow \left( {SAC} \right) \cap \left( {SMN} \right) = SO\).

