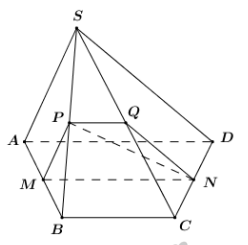
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, N, P lần lượt là trung điểm của AB, CD, SB. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {MNP} \right)\) là
41
23/04/2024
Cho hình chóp S.ABCD có ABCD là hình thang cân đáy lớn AD. Gọi M, N, P lần lượt là trung điểm của AB, CD, SB. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {MNP} \right)\) là
A. hình bình hành.
B. hình thang.
C. hình chữ nhật.
D. hình vuông.
Trả lời
Đáp án B
Phương pháp:
Dạng thiết diện có sử dụng yếu tố song song.
Cách giải:
Vì \[MN\] là đường trung bình của hình thang \(ABCD \Rightarrow MN||AD||BC\).
Ta có: \(\left\{ \begin{array}{l}\left( {MNP} \right) \supset MN\\\left( {SBC} \right) \supset BC\\MN||BC\left( {cmt} \right)\\P \in \left( {MNP} \right) \cap \left( {SBC} \right)\end{array} \right.\) Þ Giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {SBC} \right)\) là đường thẳng đi qua \(P\) và song song với \(MN,BC\).
Gọi \(Q\) là trung điểm của \(SC \Rightarrow PQ||BC\) (\(PQ\) là đường trung bình của tam giác \[SBC\]) \[ \Rightarrow \left( {MNP} \right) \cap \left( {SBC} \right) = PQ\].
Vậy thiết diện của hình chóp cắt bởi \(\left( {MNP} \right)\) là tứ giác \[MNPQ\].
Do \[PQ||BC||MN \Rightarrow MNPQ\] là hình thang.
