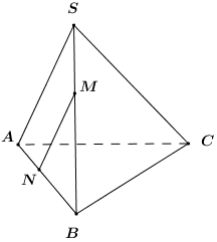
Cho hình chóp S.ABC. Lấy hai điểm M, N lần lượt nằm trên các cạnh SB, AB sao cho SM/SB = 1/4 và NB = 3NA. Khi đó, đường thẳng MN song song với mặt phẳng? A. ( SAB) B. ( SBC) C. ( ABC
Cho hình chóp S.ABC. Lấy hai điểm M, N lần lượt nằm trên các cạnh SB, AB sao cho \(\frac{{SM}}{{SB}} = \frac{1}{4}\) và \(NB = 3NA\). Khi đó, đường thẳng MN song song với mặt phẳng?
A. \(\left( {SAB} \right)\)
B. \(\left( {SBC} \right)\)
C. \(\left( {ABC} \right)\)
D. \(\left( {SAC} \right)\)