Cho hình chóp S.ABC có SA vuông góc (ABC), AI vuông góc BC (I thuộc BC), AH vuông góc SI (H thuộc SI).
Cho hình chóp S.ABC có SA ⊥ (ABC), AI ⊥ BC (I ∈ BC), AH ⊥ SI (H ∈ SI). Chứng minh rằng khoảng cách từ A đến mặt phẳng (SBC) bằng AH.
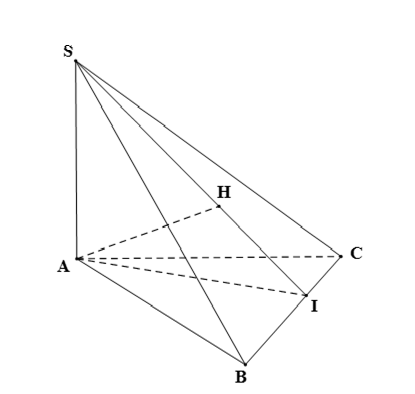
Do SA ⊥ (ABC) và BC ⊂ (ABC) nên SA ⊥ BC.
Ta có: BC ⊥ SA, BC ⊥ AI và SA ∩ AI = A trong (SAI).
Suy ra BC ⊥ (SAI).
Mà AH ⊂ (SAI) nên BC ⊥ AH.
Ta có: AH ⊥ BC, AH ⊥ SI và BC ∩ SI = I trong (SBC).
Suy ra AH ⊥ (SBC).
Ta thấy H ∈ (SBC) và AH ⊥ (SBC) nên khoảng cách từ A đến mặt phẳng (SBC) bằng AH.