Cho hình chóp S.ABCD có SA vuông góc (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).
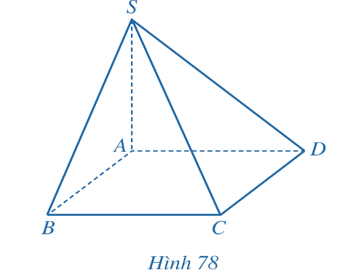
a) Tính khoảng cách từ điểm S đến đường thẳng CD.
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).

a) Tính khoảng cách từ điểm S đến đường thẳng CD.
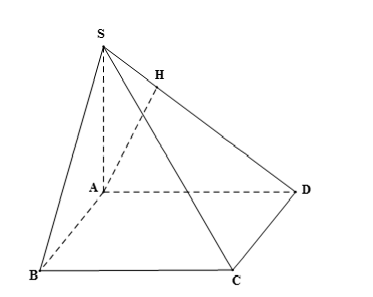
a) Do SA ⊥ (ABCD) và CD ⊂ (ABCD) nên SA ⊥ CD.
Vì ABCD là hình vuông nên CD ⊥ AD.
Ta có: CD ⊥ SA, CD ⊥ AD và SA ∩ AD = A trong (SAD).
Suy ra CD ⊥ (SAD).
Mà SD ⊂ (SAD) nên CD ⊥ SD.
Suy ra d(S, CD) = SD.
Do SA ⊥ (ABCD) và AD ⊂ (ABCD) nên SA ⊥ AD.
Áp dụng định lí Pythagore vào tam giác SAD vuông tại A (do SA ⊥ AD) có:
SD2 = SA2 + AD2 = a2 + a2 = 2a2.
Suy ra SD=a√2.
Do đó d(S,CD)=SD=a√2.
Vậy khoảng cách từ điểm S đến đường thẳng CD bằng a√2.